
分析 (1)先进行完全平方公式的运算,然后合并;
(2)根据二次根式的乘法发展和除法法则求解;
(3)先进行二次根式的化简,然后合并;
(4)先进行二次根式的化简,然后合并;
(5)先进行二次根式的除法运算和完全平方公式,然后合并;
(6)先进行二次根式的化简,然后合并.
解答 解:(1)原式=18-12$\sqrt{6}$+12-18-12$\sqrt{6}$-12
=-24$\sqrt{6}$;
(2)原式=25$\sqrt{6}$÷$\sqrt{6}$
=25;
(3)原式=4$\sqrt{3}$+3$\sqrt{3}$
=7$\sqrt{3}$;
(4)原式=4$\sqrt{3}$-3$\sqrt{3}$+6$\sqrt{3}$
=7$\sqrt{3}$;
(5)原式=3-$\sqrt{3}$-7-4$\sqrt{3}$
=-4-5$\sqrt{3}$;
(6)原式=2$\sqrt{2}$+$\sqrt{3}$-2$\sqrt{2}$
=$\sqrt{3}$.
点评 本题考查了二次根式的混合运算,解答本题的关键是掌握二次根式的化简与合并.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
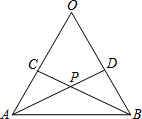 如图所示,AO=BO,CO=DO,连接AD、BC,设AD、BC相交于点P.结论:①△AOD≌△BOC;②△APC≌△BPD;③点P在∠AOB的平分线上.以上结论中( )
如图所示,AO=BO,CO=DO,连接AD、BC,设AD、BC相交于点P.结论:①△AOD≌△BOC;②△APC≌△BPD;③点P在∠AOB的平分线上.以上结论中( )| A. | 只有①正确 | B. | 只有②正确 | C. | 只有①②正确 | D. | ①②③都正确 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (-1,6) | B. | (-4,-2) | C. | (-2,6) | D. | (-2,-2) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
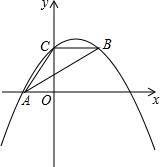 如图,抛物线y=ax2+bx+c经过A(-3.0)、C(0,4),点B在抛物线上,CB∥x轴,且AB平分∠CAO.
如图,抛物线y=ax2+bx+c经过A(-3.0)、C(0,4),点B在抛物线上,CB∥x轴,且AB平分∠CAO.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
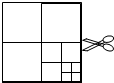 如图,将一张正方形纸片剪成四个小正方形,得到4个小正方形,称为第一次操作;然后,将其中的一个正方形再剪成四个小正方形,共得到7个小正方形,称为第二次操作;再将其中的一个正方形再剪成四个小正方形,共得到10个小正方形,称为第三次操作;…;根据以上操作,若操作670次,得到小正方形的个数是( )
如图,将一张正方形纸片剪成四个小正方形,得到4个小正方形,称为第一次操作;然后,将其中的一个正方形再剪成四个小正方形,共得到7个小正方形,称为第二次操作;再将其中的一个正方形再剪成四个小正方形,共得到10个小正方形,称为第三次操作;…;根据以上操作,若操作670次,得到小正方形的个数是( )| A. | 2009 | B. | 2010 | C. | 2011 | D. | 2012 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
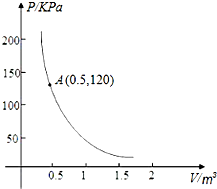 某校举行田径运动会,学校准备了某种气球,这些气球内充满了一定质量的气体,当温度不变时,气球内气体的气压P(kPa)是气体体积V(m3)的反比例函数,其图象如图所示.当气球内的气压大于150KPa时,气球会将爆炸,为了安全起见,气体的体积应不小于0.4m3.
某校举行田径运动会,学校准备了某种气球,这些气球内充满了一定质量的气体,当温度不变时,气球内气体的气压P(kPa)是气体体积V(m3)的反比例函数,其图象如图所示.当气球内的气压大于150KPa时,气球会将爆炸,为了安全起见,气体的体积应不小于0.4m3.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com