
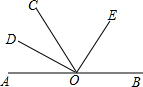
 如图所示,直线AB上有一点O,由O点引出一条射线OC,作∠AOC,∠BOC的平分线OD,OE.OD和OE垂直吗?若OC在转动,其他条件不变,上述条件成立吗?
如图所示,直线AB上有一点O,由O点引出一条射线OC,作∠AOC,∠BOC的平分线OD,OE.OD和OE垂直吗?若OC在转动,其他条件不变,上述条件成立吗? 分析 结合题意和图形,运用平角的定义和角平分线的定义,证明∠EOD是90°,得直线OE、OD的位置关系.
解答 解:垂直,理由如下:
∵射线OC把平角∠AOB分成两个角,
∴∠AOC+∠BOC=180°,
又∵OD,OE分别是∠BOC和∠AOC的平分线,
∴∠EOC=$\frac{1}{2}$∠AOC,∠DOC=$\frac{1}{2}$∠BOC,
∴∠EOD=∠EOC+∠DOC=$\frac{1}{2}$(∠BOC+∠AOC)=90°,
∴OE和OD的位置关系是垂直;
当OC在转动,其他条件不变,上述条件仍成立.
点评 此题考查垂直的定义,利用垂直的定义除了由垂直得直角外,还能由直角判定垂直,判断两直线的夹角是否为90°是判断两直线是否垂直的基本方法.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
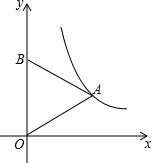 如图,等边三角形OAB的顶点A在反比例函数y=$\frac{\sqrt{3}}{x}$的图象上,点B在y轴上,若将△OAB沿x轴正方向平移,当点B落在反比例函数的图象上时,点A的坐标为($\frac{3\sqrt{3}}{2}$,1).
如图,等边三角形OAB的顶点A在反比例函数y=$\frac{\sqrt{3}}{x}$的图象上,点B在y轴上,若将△OAB沿x轴正方向平移,当点B落在反比例函数的图象上时,点A的坐标为($\frac{3\sqrt{3}}{2}$,1).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,O是等边△ABC内一点,OA=3,OB=4,OC=5,以点B为旋转中心,将线段BO逆时针旋转60°得到线段BO′,连接AO′.则下列结论:
如图,O是等边△ABC内一点,OA=3,OB=4,OC=5,以点B为旋转中心,将线段BO逆时针旋转60°得到线段BO′,连接AO′.则下列结论:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com