
����Ŀ����ֱ������ϵxOy�У�A��0��2����B����1��0��������ABO������ת��ƽ�Ʊ仯��õ���ͼ1��ʾ�ġ�BCD��
��1����A��B��C����������ߵĽ���ʽ��
��2������AC����P��λ���߶�BC�Ϸ�����������һ���㣬��ֱ��PC����ABC������ֳ�1��3�����֣����ʱ��P�����ꣻ
��3���ֽ���ABO����BCD�ֱ����¡�������1��2���ٶ�ͬʱƽ�ƣ�����ڴ��˶������С�ABO���BCD�ص�������������ֵ��

���𰸡���1��![]() ����2��P��
����2��P��![]() ��
��![]() ����P��
����P��![]() ��
��![]() ������3��
������3��![]() ��
��
��������
�����������1����A��0��2����B����1��0��������ABO������ת��ƽ�Ʊ仯�õ���BCD����BD=OA=2��CD=OB=1����BDC=��AOB=90�㣬��C��1��1����
�辭��A��B��C����������߽���ʽ![]() ������
������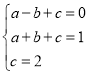 ����
����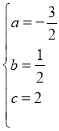 ���������߽���ʽΪ
���������߽���ʽΪ![]() ��
��
��2����ͼ1��ʾ����ֱ��PC��AB���ڵ�E����ֱ��PC����ABC������ֳ�1��3�����֣���![]() ��
��![]() ����E��EF��OB�ڵ�F����EF��OA������BEF�ס�BAO����
����E��EF��OB�ڵ�F����EF��OA������BEF�ס�BAO����![]() ������
������![]() ʱ��
ʱ��![]() ����EF=
����EF=![]() ��BF=
��BF=![]() ����E��
����E��![]() ��
��![]() ������ֱ��PC����ʽΪ
������ֱ��PC����ʽΪ![]() ����
����![]() ����
����![]() ��
��![]() ����ȥ������P��
����ȥ������P��![]() ��
��![]() ����
����
��![]() ʱ��ͬ���ɵã�P��
ʱ��ͬ���ɵã�P��![]() ��
��![]() ����
����
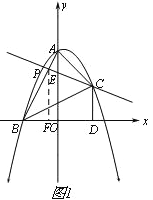
��3�����ABOƽ�Ƶľ���Ϊt����A1B1O1���B2C1D1�ص����ֵ����ΪS��
��ƽ�Ƶã�A1B1�Ľ���ʽΪy=2x+2��t��A1B1��x�ύ������Ϊ��![]() ��0����
��0����
C1B2�Ľ���ʽΪ![]() ��C1B2��y�ύ������Ϊ��0��
��C1B2��y�ύ������Ϊ��0��![]() ����
����
����ͼ2��ʾ����![]() ʱ����A1B1O1���B2C1D1�ص�����Ϊ�ı��Σ�
ʱ����A1B1O1���B2C1D1�ص�����Ϊ�ı��Σ�
��A1B1��x�ύ�ڵ�M��C1B2��y�ύ�ڵ�N��A1B1��C1B2���ڵ�Q������OQ��
����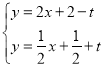 ����
����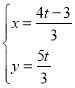 ����Q��
����Q��![]() ��
��![]() ������
������![]() =
=![]() ����S�����ֵΪ
����S�����ֵΪ![]() ��
��
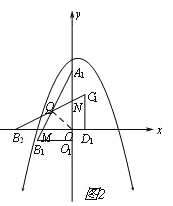
����ͼ3��ʾ����![]() ʱ����A1B1O1���B2C1D1�ص�����Ϊֱ�������Σ�
ʱ����A1B1O1���B2C1D1�ص�����Ϊֱ�������Σ�
��A1B1��x�ύ�ڵ�H��A1B1��C1D1���ڵ�G����G��1��2t��4��5t������D1H=![]() ��D1G=4��5t����S=
��D1G=4��5t����S=![]() D1H��D1G=
D1H��D1G=![]() ������
������![]() ʱ��S�����ֵΪ
ʱ��S�����ֵΪ![]() ��
��
�����������ڴ��˶������С�ABO���BCD�ص�������������ֵΪ![]() ��
��


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ij�50��ѧ���μ��������ԣ�ȫ��ѧ���ɼ��ϸ���Ϊ94%���ϸ��������___________��.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�մ��̣�Ϊ�˴���������һֻ�������һֻ�豭��ij�˹�����162Ԫ����ò���豭��36ֻ����֪ÿֻ���15Ԫ��ÿֻ�豭3Ԫ�������в�����豭������ֻ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ�����ݣ�5��7��10��5��7��5��6���������ݵ���������λ���ֱ��ǣ� ��
A.10��7B.5��7C.5��6D.6��7
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ֽƬABCD�۵���ʹ��Aǡ���������εĶԳ�����O�����ۺ�ΪEF��������ABCD�ı߳�Ϊ2cm����A=120�㣬��EF=cm��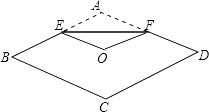
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ACB�͡�ADE��Ϊ�ȱ������Σ���C��E��D��ͬһֱ���ϣ�����BD�� ��֤��CE=BD��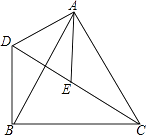
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������룺
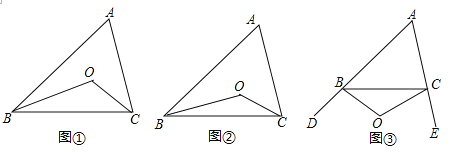
��1����ͼ�٣��ڡ�ABC�У���O�ǡ�ABC�͡�ACBƽ���ߵĽ��㣬����A=�������BOC= ���æ���ʾ������ͼ�ڣ���CBO=![]() ��ABC����BCO=
��ABC����BCO=![]() ��ACB����A=�������BOC= ���æ���ʾ��
��ACB����A=�������BOC= ���æ���ʾ��
��չ�о���
��2����ͼ�ۣ���CBO=![]() ��DBC����BCO=
��DBC����BCO=![]() ��ECB����A=����������BOC= ���æ���ʾ������˵�����ɣ�
��ECB����A=����������BOC= ���æ���ʾ������˵�����ɣ�
������
��3��BO��CO�ֱ��ǡ�ABC����ǡ�DBC����ECB��n�ȷ��ߣ����ǽ��ڵ�O����CBO=![]() ��DBC����BCO=
��DBC����BCO=![]() ��ECB����A=����������BOC= ��
��ECB����A=����������BOC= ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У���A��B������ֱ�ΪA��a��b����B��c��d��������a��c���ѵ�A ����ƽ��2��λ������ƽ��1����λ�õ�A1 �� 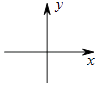
��1����A1������Ϊ ��
��2����a��b��c���� 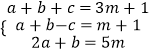 �����ú�m��ʽ�ӱ�ʾa��b��c��
�����ú�m��ʽ�ӱ�ʾa��b��c��
��3���ڣ�2����ǰ���£�����A��B�ڵ�һ������������������ϣ�S ![]() ������Ƿ�������ֵ����Сֵ��������ڣ���������ֵ����������ڣ���˵�����ɣ�
������Ƿ�������ֵ����Сֵ��������ڣ���������ֵ����������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com