
【题目】在平面直角坐标系中,点A,B的坐标分别为A(a,b)、B(c,d),其中a>c,把点A 向上平移2单位,向左平移1个单位得点A1 . 
(1)点A1的坐标为 .
(2)若a,b,c满足 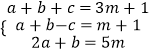 ,请用含m的式子表示a,b,c.
,请用含m的式子表示a,b,c.
(3)在(2)的前提下,若点A、B在第一象限或坐标轴的正半轴上,S ![]() 的面积是否存在最大值或最小值,如果存在,请求出这个值.如果不存在,请说明理由.
的面积是否存在最大值或最小值,如果存在,请求出这个值.如果不存在,请说明理由.
【答案】
(1)解:由平移知,点A1(a﹣1,b+2),故答案为:(a﹣1,b+2).
(2)解:∵a,b,c满足 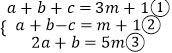 ,
,
①+②得,a+b=2m+1④,
③﹣①得,a=3m﹣1,
将a=3m﹣1代入④得,b=2m+1﹣(3m﹣1)=﹣m+2,
将a=3m﹣1,b=﹣m+2代入①得,c=3m+1﹣a﹣b=m,
即:a=3m﹣1,b=﹣m+2,c=m,
(3)解:如图,由(2)知,a=3m﹣1,b=﹣m+2,c=m,
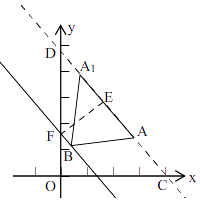
∴A(3m﹣1,﹣m+2),A1(3m﹣2,﹣m+4),B(m,d),
∵点A、B在第一象限或坐标轴的正半轴上,
∴3m﹣1≥0,﹣m+2≥0,m≥0,d≥0,
∴ ![]() ≤m≤2,d≥0,
≤m≤2,d≥0,
∵a>c,
∴3m﹣1>m,
∴m> ![]() ,
,
∴ ![]() <m≤2,
<m≤2,
即: ![]() <m≤2,d≥0,
<m≤2,d≥0,
∵A(3m﹣1,﹣m+2),A1(3m﹣2,﹣m+4),
∴直线AA1的解析式为y=﹣2x+5m,
延长AA1交x轴于C,交y轴于D,
∴D(0,5m),C( ![]() m,0),
m,0),
∴OC= ![]() m,OD=5m,
m,OD=5m,
∴CD= ![]() m,
m,
∴sin∠ODC= ![]() =
= ![]() =
= ![]() ,
,
过点B作BF∥AA1交y轴于F,
∵B(m,d),
∴直线BF得解析式为y=﹣2x+2m+d,
∴F(0,2m+d),
∴DF=|5m﹣(2m+d)|=|3m﹣d|,
过点F作FE⊥AA1于E,
在Rt△DEF中,EF=DFsin∠ODC=|3m﹣d|× ![]() ,
,
∴S△ABA1= ![]() AA1EF=
AA1EF= ![]() ×
× ![]() ×
× ![]() |3m﹣d|=
|3m﹣d|= ![]() |3m﹣d|,
|3m﹣d|,
∵ ![]() <m≤2,d≥0,
<m≤2,d≥0,
∴|3m﹣d|不存在最大值或最小值,
即:S△ABA1不存在最大值,也不存在最小值.
【解析】(1)依据上加下减,右加左减的法则进行计算即可;
(2)将三元一次方程组变为二元一次方程组,然后咋将二元一次方程组变为一元一次方程求解即可;
(3)先求出AA1的长,然后再求出点B到直线AA1得距离,然后依据三角形的面积公式得到求得S△ABA1的值,从而可作出判断.
【考点精析】本题主要考查了一次函数的图象和性质和确定一次函数的表达式的相关知识点,需要掌握一次函数是直线,图像经过仨象限;正比例函数更简单,经过原点一直线;两个系数k与b,作用之大莫小看,k是斜率定夹角,b与Y轴来相见,k为正来右上斜,x增减y增减;k为负来左下展,变化规律正相反;k的绝对值越大,线离横轴就越远;确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法才能正确解答此题.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】在直角坐标系xOy中,A(0,2)、B(﹣1,0),将△ABO经过旋转、平移变化后得到如图1所示的△BCD.
(1)求经过A、B、C三点的抛物线的解析式;
(2)连结AC,点P是位于线段BC上方的抛物线上一动点,若直线PC将△ABC的面积分成1:3两部分,求此时点P的坐标;
(3)现将△ABO、△BCD分别向下、向左以1:2的速度同时平移,求出在此运动过程中△ABO与△BCD重叠部分面积的最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点D,E分别在线段AB,AC上,CD与BE相交于O点,已知AB=AC,现添加以下的哪个条件仍不能判定△ABE≌△ACD( ) 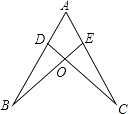
A.∠B=∠C
B.AD=AE
C.BD=CE
D.BE=CD
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB=A1B,A1B1=A1B2 , A2B2=A2B3 , A3B3=A3B4 , …若∠A=70°,则∠An的度数为( ) 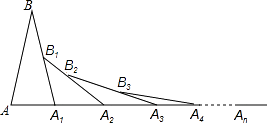
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校在基地参加社会实践话动中,带队老师考问学生:基地计划新建一个矩形的生物园地,一边靠旧墙(墙足够长),另外三边用总长69米的不锈钢栅栏围成,与墙平行的一边留一个宽为3米的出入口,如图所示,如何设计才能使园地的而积最大?下面是两位学生争议的情境:

请根据上面的信息,解决问题:
(1)设AB=x米(x>0),试用含x的代数式表示BC的长;
(2)请你判断谁的说法正确,为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,动点P在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点(1,1),第2次接着运动到点(2,0),第3次接着运动到点(3,2),…,按这样的运动规律,经过第2011次运动后,动点P的坐标是 . 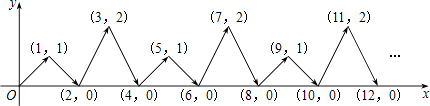
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com