
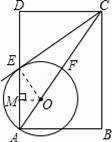
如图,在矩形ABCD中,点O在对角线AC上,以OA的长为半径的圆O与AD、AC分别交于点E、F,且∠ACB=∠DCE.
(1)判断直线CE与⊙O的位置关系,并证明你的结论;
(2)若tan∠ACB=
 ,BC=2,求⊙O的半径.
,BC=2,求⊙O的半径.
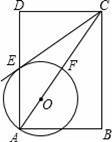

【考点】圆的综合题.
【分析】(1)连接OE.欲证直线CE与⊙O相切,只需证明∠CEO=90°,即OE⊥CE即可;
(2)在直角三角形ABC中,根据三角函数的定义可以求得AB=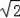
 ,然后根据勾股定理求得AC=
,然后根据勾股定理求得AC=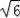
 ,同理知DE=1;
,同理知DE=1;
方法一、在Rt△COE中,利用勾股定理可以求得CO2=OE2+CE2,即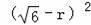
 =r2+3,从而易得r的值;
=r2+3,从而易得r的值;
方法二、过点O作OM⊥AE于点M,在Rt△AMO中,根据三角函数的定义可以求得r的值.
【解答】解:(1)直线CE与⊙O相切.…
理由如下:
∵四边形ABCD是矩形,
∴BC∥AD,∠ACB=∠DAC;
又∵∠ACB=∠DCE,
∴∠DAC=∠DCE;
连接OE,则∠DAC=∠AEO=∠DCE;
∵∠DCE+∠DEC=90°
∴∠AE0+∠DEC=90°
∴∠OEC=90°,即OE⊥CE.
又OE是⊙O的半径,
∴直线CE与⊙O相切.…
(2)∵tan∠ACB=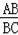
 =
=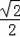
 ,BC=2,
,BC=2,
∴AB=BC•tan∠ACB=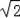
 ,
,
∴AC=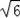
 ;
;
又∵∠ACB=∠DCE,
∴tan∠DCE=tan∠ACB=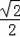
 ,
,
∴DE=DC•tan∠DCE=1;
方法一:在Rt△CDE中,CE=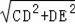
 =
=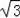
 ,
,
连接OE,设⊙O的半径为r,则在Rt△COE中,CO2=OE2+CE2,即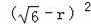
 =r2+3
=r2+3
解得:r=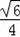

方法二:AE=AD﹣DE=1,过点O作OM⊥AE于点M,则AM=
 AE=
AE=

在Rt△AMO中,OA=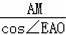
 =
=
 ÷
÷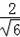
 =
=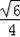
 …
…

【点评】本题考查了圆的综合题:圆的切线垂直于过切点的半径;利用勾股定理计算线段的长.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
如图,已知AB=A1B,在AA1的延长线上依次取A2、A3、A4、…、An,并依次在三角形的外部作等腰三角形,使A1C1=A1A2,A2C2=A2A3,A3C3=A3A4,…,An﹣1Cn﹣1=An﹣1An,若∠B=30°,则∠An= °.

查看答案和解析>>
科目:初中数学 来源: 题型:
元旦游园晚会上,有一个闯关活动:将20个大小重量完全要样的乒乓球放入一个袋中,其中8个白色的,5个黄色的,5个绿色的,2个红色的.如果任意摸出一个乒乓球是红色,就可以过关,那么一次过关的概率为( )
A.
 B.
B.
 C.
C.
 D.
D.

查看答案和解析>>
科目:初中数学 来源: 题型:
某商店需要购进甲、乙两种商品共160件,其进价和售价如下表:
|
| 甲 | 乙 |
| 进价(元/件) | 15 | 35 |
| 售价(元/件) | 20 | 45 |
(1)若商店计划销售完这批商品后能获利1100元,问甲、乙两种商品应分别购进多少件?
(2)若商店计划投入资金少于4300元,且销售完这批商品后获利多于1260元,请问有哪几种购货方案?并直接写出其中获利最大的购货方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
如图所示,宽为50 cm的矩形图案由10个全等的小长方形拼成,其中一个小长方形的面积为( ).

A.400 cm2 B.500 cm2  C.600 cm2 D.4 000 cm2
C.600 cm2 D.4 000 cm2
查看答案和解析>>
科目:初中数学 来源: 题型:
小华不小心将墨水溅在同桌小丽的作业本上,结果二元一次方程组 中第一个方程y的系数和第二个方程x的系数看不到了,现在已知小丽的结果是
中第一个方程y的系数和第二个方程x的系数看不到了,现在已知小丽的结果是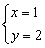 ,你能由此求出原来的方程组吗?
,你能由此求出原来的方程组吗?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com