练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    3．已知b＜a＜0，则ab，a2，b2的大小为a2＜ab＜b2．

    分析 利用不等式的性质，由b＜a＜0，可得ab＞a2，b2＞ab，由此即可判断．

    解答 解：∵b＜a＜0，
    ∴ab＞a2，b2＞ab，
    ∴a2＜ab＜b2，
    故答案为a2＜ab＜b2．

    点评 本题考查有理数的大小比较、不等式的性质等知识，解题的关键是灵活应用不等式的性质解决问题，属于基础题，中考常考题型．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    2．如图：在边长为1的正方形网格中有一个△ABC，按要求进行下列解答：
    （1）△ABC的面积为3；
    （2）画出先将△ABC向右平移6格，再向上平移3格后的△DEF；
    （3）画出△ABC绕点B顺时针旋转90°后的图形；
    （4）画出△ABC沿直线EF翻折后的图形．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    3．计算；
    （1）$\sqrt{24}$+2$\sqrt{\frac{2}{3}}$-3$\sqrt{\frac{3}{2}}$；
    （2）$\sqrt{75}$-$\sqrt{54}$÷$\sqrt{2}$+（3-$\sqrt{3}$）（1+$\frac{1}{\sqrt{3}}$）
    （3）$\sqrt{18}$+（3+2$\sqrt{3}$）（2$\sqrt{3}$-3）-$\sqrt{\frac{3}{2}}$×$\sqrt{48}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    20．如图，在平行四边形ABCD中，DE⊥AB，DF⊥BC，垂足分别为E，F，AB=8，AD=6．
    （1）求$\frac{DE}{DF}$的值；
    （2）若∠A=60°，求△EDF的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    7．已知点A（-6，y1）和B（-2，y2）都在直线y=-$\frac{1}{3}$x+b上，则y1，y2的大小关系是（　　）
    A．y1＞y2B．y1＜y2C．y1=y2D．大小不确定

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    8．如图表示的是一个蒙古包，该蒙古包近似地看作是几何体（　　）
    A．圆锥和长方体的组合B．圆锥和圆柱的组合
    C．圆锥和正方体的组合D．四面体和圆柱的组合

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

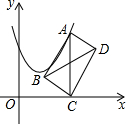    15．如图，在平面直角坐标系中，点A在抛物线y=x2-2x+2上运动，点C在x轴上运动，以AC为对角线作矩形ABCD，连结BD，则对角线BD的最小值为（　　）
    A．$\frac{\sqrt{2}}{2}$B．1C．$\sqrt{2}$D．2

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    12．如图，在平面直角坐标系中，边长为2的等边△CDE恰好与坐标系中的△OAB重合，现将△CDE绕边AB的中点G（G也是DE的中点），按顺时针方向旋转180°到△C′DE的位置．
    （1）求C′点的坐标；
    （2）求经过三点O、A、C′的抛物线的解析式；
    （3）如图③，⊙G是以AB为直径的圆，过B点作⊙G的切线与x轴交于点F，求切线BF的解析式；
    （4）在（3）的条件下，直线BF与抛物线交于M、N两点，P是MN上的动点，过P作x轴的垂线交抛物线于Q，求PQ的最大长度．

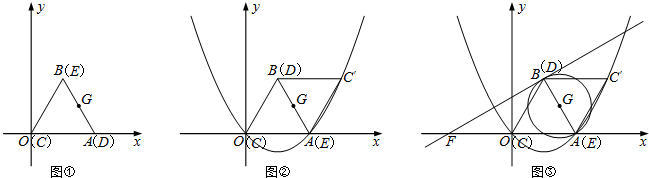
    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    13．计算
    （1）（-2）+4+（-8）+6；
    （2）$\frac{1}{2}$+（-$\frac{2}{3}$）-（-$\frac{1}{3}$）+（+$\frac{1}{4}$）；
    （3）-14÷（-52）×（-$\frac{5}{3}$）+|0.8-1|；       
    （4）（-27）÷（-3）×$\frac{1}{3}$．

    查看答案和解析>>

    同步练习册答案