
����Ŀ����֪��ABD����GDF���ǵ���ֱ�������Σ�BD��DF��Ϊб�ߣ�BD��DF����
��1����ͼ1��B��D��F��ͬһֱ���ϣ���F��MF��GF�ڵ�F��ȡMF=AB������AM��BF�ڵ�H������GA��GM��
����֤��AH=HM��
�����ж���GAM����״��������֤����
�����õ�ʽ��ʾ�߶�AM��BD��DF��������ϵ����˵�����ɣ�
��2����ͼ2��GD��BD������BF��ȡBF���е�H������AH���ӳ���DF�ڵ�M�����õ�ʽֱ��д���߶�AM��BD��DF��������ϵ��

���𰸡���1��������������������������2��AM2=BD2+DF2��![]() DFBD��
DFBD��
��������
��1������֤��ABD=��HFM=45�����Ӷ����ݡ�AAS����֤��AHB�ա�MHF����ȫ�������εĶ�Ӧ����ȿɵ�AH=HM��
�ڸ��ݡ�SAS����֤��GAD�ա�GMF���Ӷ�AG=GM����AGD=��MGF��������֤��AGM=90��,������GAM�ǵ���ֱ����������
�۸��ݹ��ɶ������ɵó��߶�AM��BD��DF��������ϵ��
��2����֤��ADM=90�������ݡ�AAS����֤��ABH�ա�HFM���Ӷ�FM=AB��Ȼ�����AM2=AD2+DM2��������.
��1����֤������ͼ1����MF��GF��
���GFM=90�㣬
�ߡ�ABD����GDF���ǵ���ֱ�������Σ�
���DFG=��ABD=45�㣬
���HFM=90�㩁45��=45�㣬
���ABD=��HFM��
��AB=MF����AHB=��MHF��
���AHB�ա�MHF��
��AH=HM��
����ͼ1����GAM�ǵ���ֱ�������Σ������ǣ�
�ߡ�ABD����GDF���ǵ���ֱ�������Σ�
��AB=AD��DG=FG��
��ADB=��GDF=45�㣬
���ADG=��GFM=90�㣬
��AB=FM��
��AD=FM��
���GAD�ա�GMF��
��AG=GM����AGD=��MGF��
���ADG+��DGM=��MGF+��DGM=90�㣬
���GAM�ǵ���ֱ�������Σ�
����ͼ1��AM2=BD2+DF2�������ǣ�
�ߡ�AGM�ǵ���ֱ�������Σ�
��AM2=2MG2��
Rt��GMF��MG2=FG2+FM2=AB2+FG2��
�ߡ�ABD����GDF���ǵ���ֱ�������Σ�
��AB=![]() ��FG=
��FG=![]() ��
��
��AM2=2MG2=2��![]() +
+![]() ��=BD2+DF2��
��=BD2+DF2��
��2����ͼ2����GD��BD����ADB=45�㣬
���ADG=45�㣬
���ADM=45��+45��=90�㣬
�ߡ�HMF=��ADM+��DAM=90��+��DAM=��BAH��
��H��BF���е㣬
��BH=HF��
�ߡ�AHB=��MHF��
���ABH�ա�HFM��
��FM=AB��
��Rt��ADM�У��ɹ��ɶ����ã�AM2=AD2+DM2��
=AD2+��DF��FM��2��
=AD2+DF2��2DFFM+FM2��
=BD2+DF2��2DF![]() ��
��
=BD2+DF2��![]() DFBD��
DFBD��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У���![]() ������Ϊ
������Ϊ![]() .
.
��1����ͼ1������![]() ������Ϊ
������Ϊ![]() ��
��![]() �ǵ���ֱ�������Σ�
�ǵ���ֱ�������Σ�![]() ��
��![]() ����
����![]() �����ꣻ
�����ꣻ

��2����ͼ2������![]() ��
��![]() ���е㣬��֤��
���е㣬��֤��![]() ��
��

��3����ͼ3��![]() �ǵ���ֱ�������Σ�
�ǵ���ֱ�������Σ�![]() ��
��![]() ��
��![]() �ǵȱ������Σ�����
�ǵȱ������Σ�����![]() ����
����![]() ����
����![]() ������.
������.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ,Rt��ACB��,��ACB=90����AC=BC��E��Ϊ����CB��һ���㣬����AE����AF��AE��AF=AE.

(1)��ͼ1����F����FD��AC��AC��D�㣬��֤��EC+CD=DF��
(2)��ͼ2,����BF��AC��G��,��![]() =3����֤��E��ΪBC�е㣻
=3����֤��E��ΪBC�е㣻
(3)��E��������CB��,����BF��ֱ��AC����G��,��![]() ,��
,��![]() =_______
=_______
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪�ڡ�ABC�У�AB=AC��DΪBC�ߵ��е㣬����D��DE��AB��DF��AC������ֱ�ΪE��F��

��1����֤��DE=DF��
��2������A=60�㣬BE=1�����ABC���ܳ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����κ���y=��m+1��x2��2��m+1��x��m+3��
��1����ö��κ����ĶԳ��
��2��������C��0��n����ֱ��l��y�ᣬ��ֱ��l��������ֻ��һ��������ʱ����n����m�ĺ�������ʽ��
��3��������ÿһ��������xֵ��������Ӧ�ĺ���ֵ��������6��������m��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������M��y��������������һ�㣬����M��PQ��x�ᣬ�ֱ���y=![]() ��x��0����y=
��x��0����y=![]() ��x��0����ͼ���ڵ�P��Q������OP��OQ�������н��ۣ�
��x��0����ͼ���ڵ�P��Q������OP��OQ�������н��ۣ�
�١�POQ�����ܵ���90�㣻
��![]() ��
��
��������������ͼ��һ������y��Գƣ�
����S��POM=S��QOM����k1+k2=0��
�ݡ�POQ�������![]() ��|k1|+|k2|����
��|k1|+|k2|����
������ȷ����_____����д��ţ���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
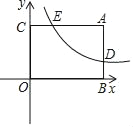
����Ŀ����ͼ��ʾ����֪����ABOC�У�AC=4��˫����y=![]() ���������AB��AC�ֱ���D��E��EΪAC���е㣮
���������AB��AC�ֱ���D��E��EΪAC���е㣮
��1�����E�����ꣻ
��2����P���߶�OB�ϵ�һ�����㣬�Ƿ���ڵ�P��ʹ��DPC=90�㣿�����ڣ������ʱ��P�����꣬�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ھ���ABCD�У�AB=6��BC=8����M��Nͬʱ�ӵ�B�������ֱ���BC��BA���˶�������M���˶��ٶ���ÿ��2����λ���ȣ����ǵ�N�˶��ٶȵ�2����������һ���㵽���յ�ʱ��ֹͣһ���˶�����MNΪ�Գ�������MNB�ĶԳ�ͼ�Ρ�MNB1����B1ǡ����AD�ϵ�ʱ��Ϊ______�룮�������˶������У���MNB1�����ABCD�ص�������������ֵΪ______��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���ABCD�У���B=��C=90����E��BC���е㣬DEƽ�֡�ADC��

(1)��֤��AEƽ����BAD��
(2)��֤��AD��AB��CD��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com