
【题目】如图,Rt△ACB中,∠ACB=90°,AC=BC,E点为射线CB上一动点,连接AE,作AF⊥AE且AF=AE.

(1)如图1,过F点作FD⊥AC交AC于D点,求证:EC+CD=DF;
(2)如图2,连接BF交AC于G点,若![]() =3,求证:E点为BC中点;
=3,求证:E点为BC中点;
(3)当E点在射线CB上,连接BF与直线AC交于G点,若![]() ,则
,则![]() =_______
=_______
【答案】(1)答案见解析;(2)答案见解析;(3)![]() .
.
【解析】
(1)通过全等三角形△ADF≌△EDA的对应边相等得到:AD=CD,FD=AC,则利用等量代换和图形中相关线段间的和差关系证得结论;
(2)过F点作FD⊥AC交AC于D点,根据(1)中结论可得FD=AC=BC,即可证明△FGD≌△BCD,可得DG=CG,根据![]() =3可证
=3可证![]() ,根据AD=CE,AC=BC,即可解题;(3)过F作FD⊥AG的延长线交于点D,易证
,根据AD=CE,AC=BC,即可解题;(3)过F作FD⊥AG的延长线交于点D,易证![]() ,由(1)(2)可知△ADF≌△ECA,△GDF≌△GCB,可得CG=GD,AD=CE,即可求得
,由(1)(2)可知△ADF≌△ECA,△GDF≌△GCB,可得CG=GD,AD=CE,即可求得![]() 的值,即可解题.
的值,即可解题.
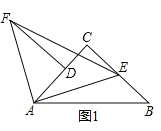
证明:(1)如图1,∵∠FAD+∠CAE=90°,∠FAD+∠F=90°,
∴∠CAE=∠AFD,
在△ADF和△ECA中,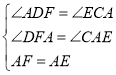 ,
,
∴△ADF≌△ECA(AAS),
∴AD=CD,FD=AC,
∴CE+CD=AD+CD=AC=FD,即EC+CD=DF;
证明:(2)如图2,
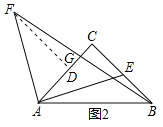
过F点作FD⊥AC交AC于D点,
∵△ADF≌△ECA,
∴FD=AC=BC,
在△FDG和△BCG中,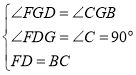 ,
,
∴△FDG≌△BCG(AAS),
∴GD=CG,
∵![]() =3
=3
∴![]()
∴![]() ,
,
∵AD=CE,AC=BC
∴![]() ,
,
∴E点为BC中点;
(3)过F作FD⊥AG的延长线交于点D,如图3,
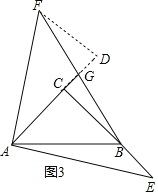
∵![]() ,BC=AC,CE=CB+BE,
,BC=AC,CE=CB+BE,
∴![]() ,
,
由(1)(2)知:△ADF≌△ECA,△GDF≌△GCB,
∴CG=GD,AD=CE,
∴![]() ,
,
∴![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
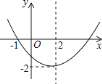
【题目】已知二次函数![]() 的图象如图所示,则下列结论:
的图象如图所示,则下列结论:
①![]() ,
,![]() 同号;②当
同号;②当![]() 和
和![]() 时,函数值相等;③
时,函数值相等;③![]() ;④当
;④当![]() 时,
时,![]() 的值只能取
的值只能取![]() ;⑤当
;⑤当![]() 时,
时,![]() .其中正确的有( )
.其中正确的有( )
A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是一辆小汽车与墙平行停放的平面示意图,汽车靠墙一侧OB与墙MN平行且距离为0.8米,一辆小汽车车门宽AO为1.2米,当车门打开角度∠AOB为40°时,车门是否会碰到墙?______;(填“是”或“否”)请简述你的理由_______.(参考数据:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,二次函数y=x2﹣2hx+h的图象的顶点为点D.
(1)当h=﹣1时,求点D的坐标;
(2)当﹣1≤x≤1时,求函数的最小值m.(用含h的代数式表示m)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是抛物线![]() 图象的一部分,抛物线的顶点坐标
图象的一部分,抛物线的顶点坐标![]() ,与
,与![]() 轴的一个交点
轴的一个交点![]() ,直线
,直线![]() 与抛物线交于
与抛物线交于![]() ,
,![]() 两点,下列结论:
两点,下列结论:
①![]() ;
;
②![]() ;
;
③方程![]() 有两个相等的实数根;
有两个相等的实数根;
④抛物线与![]() 轴的另一个交点是
轴的另一个交点是![]() ;
;
⑤当![]() 时,有
时,有![]() .
.
其中正确结论的个数是( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AB=AD,CB=CD,对角线AC,BD相交于点O,下列结论中:
①∠ABC=∠ADC;
②AC与BD相互平分;
③AC,BD分别平分四边形ABCD的两组对角;
④四边形ABCD的面积S=![]() ACBD.
ACBD.
正确的是 (填写所有正确结论的序号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABD与△GDF都是等腰直角三角形,BD与DF均为斜边(BD<DF).
(1)如图1,B,D,F在同一直线上,过F作MF⊥GF于点F,取MF=AB,连结AM交BF于点H,连结GA,GM.
①求证:AH=HM;
②请判断△GAM的形状,并给予证明;
③请用等式表示线段AM,BD,DF的数量关系,并说明理由.
(2)如图2,GD⊥BD,连结BF,取BF的中点H,连结AH并延长交DF于点M,请用等式直接写出线段AM,BD,DF的数量关系.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,E、F分别是AB、BC边的中点,EP⊥CD于点P,∠BAD=110°,则∠FPC的度数是( )

A. 35° B. 45° C. 50° D. 55°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com