
【题目】如图,是一辆小汽车与墙平行停放的平面示意图,汽车靠墙一侧OB与墙MN平行且距离为0.8米,一辆小汽车车门宽AO为1.2米,当车门打开角度∠AOB为40°时,车门是否会碰到墙?______;(填“是”或“否”)请简述你的理由_______.(参考数据:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84)

科目:初中数学 来源: 题型:
【题目】(1)如图1,Rt△ABC中,若AC=4,BC=3,DE⊥AC,且DE=DB,求AD的长;
(2)如图2,已知△ABC,若AB边上存在一点M,若AC边上存在一点N,使MB=MN,且△AMN∽△ABC,请利用没有刻度的直尺和圆规,作出符合条件的线段MN(注:不写作法,保留作图痕迹,对图中涉及到的点用字母进行标注).
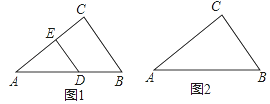
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点![]() 的坐标为
的坐标为![]() .
.
(1)如图1,若点![]() 的坐标为
的坐标为![]() ,
,![]() 是等腰直角三角形,
是等腰直角三角形,![]() ,
,![]() ,求
,求![]() 点坐标;
点坐标;

(2)如图2,若点![]() 是
是![]() 的中点,求证:
的中点,求证:![]() ;
;

(3)如图3,![]() 是等腰直角三角形,
是等腰直角三角形,![]() ,
,![]() ,
,![]() 是等边三角形,连接
是等边三角形,连接![]() ,若
,若![]() ,求
,求![]() 点坐标.
点坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,∠B=∠C=90°,AB>CD,AD=AB+CD.
(1)利用尺规作∠ADC的平分线DE,交BC于点E,在AD上截取AF=AB,连接AE.EF(保留作图痕迹,不写作法);
(2)在(l)的条件下,求证:EC=EF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是小明利用等腰直角三角板测量旗杆高度的示意图.等腰直角三角板的斜边BD与地面AF平行,当小明的视线恰好沿BC经过旗杆顶部点E时,测量出此时他所在的位置点A与旗杆底部点F的距离为10米.如果小明的眼睛距离地面1.7米,那么旗杆EF的高度为( )

A. 10米 B. 11.7米 C. 10![]() 米 D. (5
米 D. (5![]() +1.7)米
+1.7)米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)在图中作出△ABC关于直线m对称的△A′B′C′,并写出A′、B′、C′三点的坐标(2)猜想:坐标平面内任意点P(x,y)关于直线m对称点P′的坐标为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ACB中,∠ACB=90°,AC=BC,E点为射线CB上一动点,连接AE,作AF⊥AE且AF=AE.

(1)如图1,过F点作FD⊥AC交AC于D点,求证:EC+CD=DF;
(2)如图2,连接BF交AC于G点,若![]() =3,求证:E点为BC中点;
=3,求证:E点为BC中点;
(3)当E点在射线CB上,连接BF与直线AC交于G点,若![]() ,则
,则![]() =_______
=_______
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:已知在△ABC中,AB=AC,D为BC边的中点,过点D作DE⊥AB,DF⊥AC,垂足分别为E,F.

(1)求证:DE=DF;
(2)若∠A=60°,BE=1,求△ABC的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=6,BC=8,点M,N同时从点B出发,分别在BC,BA上运动,若点M的运动速度是每秒2个单位长度,且是点N运动速度的2倍,当其中一个点到达终点时,停止一切运动.以MN为对称轴作△MNB的对称图形△MNB1.点B1恰好在AD上的时间为______秒.在整个运动过程中,△MNB1与矩形ABCD重叠部分面积的最大值为______.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com