
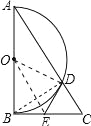
【题目】如图,Rt△ABC中,∠ABC=90°,以AB为直径作半圆⊙O交AC与点D,点E为BC的中点,连接DE.
(1)求证:DE是半圆⊙O的切线.
(2)若∠BAC=30°,DE=2,求AD的长.

【答案】(1)证明详见解析;(2)6.
【解析】
试题分析:(1)连接OD,OE,由AB为圆的直径得到三角形BCD为直角三角形,再由E为斜边BC的中点,得到DE=BE=DC,再由OB=OD,OE为公共边,利用SSS得到三角形OBE与三角形ODE全等,由全等三角形的对应角相等得到DE与OD垂直,即可得证;
(2)在直角三角形ABC中,由∠BAC=30°,得到BC为AC的一半,根据BC=2DE求出BC的长,确定出AC的长,再由∠C=60°,DE=EC得到三角形EDC为等边三角形,可得出DC的长,由AC﹣CD即可求出AD的长.
试题解析:(1)连接OD,OE,BD,
∵AB为圆O的直径,
∴∠ADB=∠BDC=90°,
在Rt△BDC中,E为斜边BC的中点,
∴DE=BE,
在△OBE和△ODE中,
OB=OD,OE=OE,BE=DE,
∴△OBE≌△ODE(SSS),
∴∠ODE=∠ABC=90°,
则DE为圆O的切线;
(2)在Rt△ABC中,∠BAC=30°,
∴BC=![]() AC,
AC,
∵BC=2DE=4,
∴AC=8,
又∵∠C=60°,DE=CE,
∴△DEC为等边三角形,即DC=DE=2,
则AD=AC﹣DC=6.


 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】“阅读让自己内心强大,勇敢面对抉择与挑战.”某校倡导学生读书,下面的表格是该校九年级学生本学期内阅读课外书籍情况统计表.请你根据统计表中提供的信息,求出表中a、b的值:a=_____,b=_____.
图书种类 | 频数 | 频率 |
科普常识 | 210 | b |
名人传记 | 204 | 0.34 |
中外名著 | a | 0.25 |
其他 | 36 | 0.06 |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知Rt△AOB的两直角边OA、OB分别在x轴的负半轴和y轴的正半轴上,且OA、OB的长满足|OA﹣8|+(OB﹣6)2=0,∠ABO的平分线交x轴于点C过点C作AB的垂线,垂足为点D,交y轴于点E.
(1)求线段AB的长;
(2)求直线CE的解析式;
(3)若M是射线BC上的一个动点,在坐标平面内是否存在点P,使以A、B、M、P为顶点的四边形是矩形?若存在,请直接写出点P的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
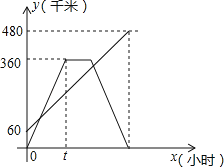
【题目】甲、乙两车分别从相距480km的A、B两地相向而行,乙车比甲车先出发1小时,并以各自的速度匀速行驶,途径C地,甲车到达C地停留1小时,因有事按原路原速返回A地.乙车从B地直达A地,两车同时到达A地.甲、乙两车距各自出发地的路程y(千米)与甲车出发所用的时间x(小时)的关系如图,结合图象信息解答下列问题:
(1)乙车的速度是 千米/时,t= 小时;
(2)求甲车距它出发地的路程y与它出发的时间x的函数关系式,并写出自变量的取值范围;
(3)直接写出乙车出发多长时间两车相距120千米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果将抛物线y=x2+2向左平移1个单位,那么所得新抛物线的表达式是( )
A. y=x2+1B. y=x2+3C. y=(x﹣1)2+2D. y=(x+1)2+2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com