练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    5．已知关于x的方程9x-3=kx+14有正整数解，那么满足条件的所有整数k=8或-8．

    分析 把k看做已知数表示出方程的解，根据方程解为正整数确定出整数k的值即可．

    解答 解：方程整理得：x=$\frac{17}{9-k}$，
    由x为正整数，得到9-k=1或9-k=17，
    解得：k=8或-8，
    故答案为：8或-8

    点评 此题考查了解二元一次方程，将k看做已知数表示出x是解本题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    15．计算m4×m4的结果是（　　）
    A．m8B．m16C．m0D．2m4

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    16．已知n＞1，M=$\frac{n}{n-1}$，N=$\frac{n-1}{n}$，P=$\frac{n}{n+1}$，则M、N、P的大小关系为M＞P＞N．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    13．不等式3x+1＜2-2（x-2）的解集在数轴上表示为（　　）
    A．B．C．D．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

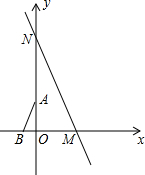    20．如图，在直角坐标系中，直线y=-$\sqrt{3}x+5\sqrt{3}$分别与x轴、y轴交于点M、N，点A、B分别在y轴、x轴上，且∠B=60°，AB=2，将△ABO绕原点O顺时针转动一周，当AB与直线MN平行时点A的坐标为（-$\frac{3}{2}$，$\frac{\sqrt{3}}{2}$）或（$\frac{3}{2}$，-$\frac{\sqrt{3}}{2}$）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    10．已知a、b满足$\sqrt{4a-b+1}$+$\sqrt{\frac{1}{3}b-4a-3}$=0，求2a（$\sqrt{\frac{b}{a}}$÷$\sqrt{\frac{1}{-b}}$）

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    17．如图，将一副三角板放在一块，AC与EF所夹的钝角的度数为165°．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    14．先因式分解，再求值：15x2（y+4）-30x（y+4），其中x=$\frac{13}{5}$，y=-$\frac{7}{3}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

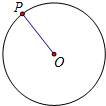    15．如图所示，⊙O的面积为1，点P为⊙O上一点，令记号[n，m]表示半径OP从如图所示的位置开始以点O为中心连续旋转n次后，半径OP扫过的面积．旋转的规则为：第1次旋转m度；第2次从第1次停止的位置向相同的方向再次旋转$\frac{m}{2}$度；第3次从第2次停止的位置向相同的方向再次旋转$\frac{m}{4}$度；第4次从第3次停止的位置向相同的方向再次旋转$\frac{m}{8}$度；…依此类推．例如[2，90]=$\frac{3}{8}$，则[2016，180]=$\frac{{2}^{2016}-1}{{2}^{2016}}$．

    查看答案和解析>>

    同步练习册答案