
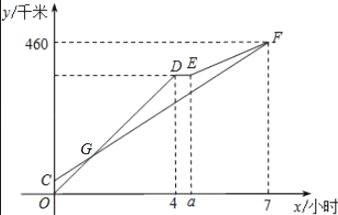
����Ŀ���ס���������A�س�����ͬһ·��ʻ��B�أ��׳��ȳ�������ʻ��B�أ�40���Ӻ��ҳ�������������ʻһ��ʱ�����;�еĻ�վװ����ʱ��Сʱ���������ػ��Ϊ����ʻ��ȫ���ٶȼ�����50ǧ��/ʱ�������׳�ͬʱ����B�أ�����������A�ص�·��y��ǧ�ף����ҳ���ʻʱ��x��Сʱ��֮��ĺ���ͼ����ͼ��ʾ��
����ͼ����Ϣ����������⣺
��1��ֱ��д��a��ֵ������׳����ٶȣ�
��2����ͼ���߶�EF����ʾ��y��x�ĺ�����ϵʽ����ֱ��д���Ա���x��ȡֵ��Χ��
��3���ҳ���������Сʱ��׳����15ǧ�ף�ֱ��д���𰸣�
���𰸡���1��4.5��60��2��y=40x+180��4.5��x��7����3��![]() Сʱ��
Сʱ��![]() Сʱ��
Сʱ��![]() Сʱ
Сʱ
���������⣺��1��a=4.5��
�׳����ٶ�=![]() =60��ǧ��/Сʱ����
=60��ǧ��/Сʱ����
��2�����ҿ�ʼ���ٶ�Ϊvǧ��/Сʱ��
��4v+��7��4.5����v��50��=460�����v=90��ǧ��/Сʱ����
4v=360��
��D��4��360����E��4.5��360����
��ֱ��EF�Ľ���ʽΪy=kx+b��
��E��4.5��360����F��7��460�������![]() ��
��
���![]() ��
��
�����߶�EF����ʾ��y��x�ĺ�����ϵʽΪy=40x+180��4.5��x��7����
��3���׳�ǰ40���ӵ�·��Ϊ60��![]() =40ǧ�ף���C��0��40����
=40ǧ�ף���C��0��40����
��ֱ��CF�Ľ���ʽΪy=mx+n��
��C��0��40����F��7��460�������![]() �����
�����![]() ��
��
����ֱ��CF�Ľ���ʽΪy=60x+40��
��ֱ��OD�Ľ���ʽΪy=90x��0��x��4����
�����������;������ΪG����60x+40=90x�����x=![]() Сʱ�����ҳ�����
Сʱ�����ҳ�����![]() Сʱ��������������
Сʱ��������������
���ҳ���OG��ʱ����60x+40��90x=15�����x=![]() ������0��
������0��![]() Сʱ֮�䣬�������⣻
Сʱ֮�䣬�������⣻
���ҳ���GD��ʱ����90x����60x+40��=15�����x=![]() ������
������![]() ��4Сʱ֮�䣬�������⣻
��4Сʱ֮�䣬�������⣻
���ҳ���DE��ʱ����360����60x+40��=15�����x=![]() ��������4��4.5֮�䣬���������⣻
��������4��4.5֮�䣬���������⣻
���ҳ���EF��ʱ����40x+180����60x+40��=15�����x=![]() ������4.5��7֮�䣬�������⣮
������4.5��7֮�䣬�������⣮
�����ҳ�����![]() Сʱ��
Сʱ��![]() Сʱ��
Сʱ��![]() Сʱ������׳����15ǧ�ף�
Сʱ������׳����15ǧ�ף�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ͼ����ʾ��10��ͬѧƽ��ÿ�������Ķ��������ʱ������ڿ����ӵ�ʱ�䣨��λ��Сʱ����
��1��������ʵ���Ա�ʾͼ�и��㡣
��2��ͼ����һ����λ�ڷ���ĶԽ����ϣ����ʾʲô��˼��
��3��ͼ�з���ֽ�ĶԽ��ߵ����Ϸ��ĵ���ʲô��ͬ���ص㣿�����·��ĵ��أ�
��4������һ����ÿ�������Ķ��������ʱ������ڿ����ӵ�ʱ�䣬��ͼ��������������λ��ʲôλ�ã�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪����y=�� ![]() x+4��ͼ����������Ľ���ֱ�Ϊ��A��B����C���B����x��Գƣ�����P��Q�ֱ����߶�BC��AB�ϣ���P�����B��C�غϣ����ҡ�APQ=��ABO
x+4��ͼ����������Ľ���ֱ�Ϊ��A��B����C���B����x��Գƣ�����P��Q�ֱ����߶�BC��AB�ϣ���P�����B��C�غϣ����ҡ�APQ=��ABO
��1����A������Ϊ �� AC�ij�Ϊ��
��2���жϡ�BPQ���CAP�Ĵ�С��ϵ����˵�����ɣ�
��3������APQΪ����������ʱ�����P�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�ǵȱ������Σ�AQ=PQ��PR��AB�ڵ�R��PS��AC�ڵ�S��PR=PS�������н��ۣ��ٵ�P�ڡ�A�Ľ�ƽ�����ϣ� ��AS=AR�� ��QP��AR�� �ܡ�BRP�ա�QSP����ȷ���У� �� 
A.1��
B.2��
C.3��
D.4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ѡ���У���������֤�����⡰��a>1,��a��1���Ǽ�����ķ������� ��
A. a=��2. B. a==��1 C. a=1 D. a=2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������˵���У���ȷ�����У�������
�ٶԶ�����ȣ�
����ֱ��ƽ�У�ͬ���ڽ���ȣ�
�۶Խ����ഹֱ���ı���Ϊ���Σ�
�ܶԽ����ഹֱƽ������ȵ��ı���Ϊ�����Σ�
A. 1�� B. 2�� C. 3�� D. 4��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com