练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

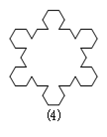
    【题目】如图，第（1）个多边形由正三角形“扩展”而来，边数记为a3，第（2）个多边形由正方形“扩展”而来，边数记为a4，……，依此类推，由正n边形“扩展”而来的多边形的边数记为an（n≥3）．则当an＝90时，n的值是_________．

    【答案】9

    【解析】分析：第一个图形的边长是把正三角形的三边都减去1后，再加上2所得，第二个图形的边长是把正方形的四边都减去1后，再加上3所得，后面都是这个规律，由此列方程求解.

    详解：由图可知中：

    (1)a3＝3(3－1＋2)＝12；

    (2)a4＝4(3－1＋3)＝20；

    (3)a5＝5(3－1＋4)＝30；

    (4)a6＝6(3－1＋5)＝42；

    ……

    则an＝n(3－1＋n－1)＝n(n＋1).

    所以n(n＋1)＝90，解得n＝9或n＝－10(舍).

    故答案为9.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】商场出售的A型冰箱每台售价2190元，每日耗电量为1度，而B型节能冰箱每台售价虽比A型冰箱高出10%，但每日耗电量却为0.55度，现将A型冰箱打折出售，商场最少打几折消费者购买才合算？（按使用期为10年，每年365天，每度电0.40元计算）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】一个正方体礼盒如图所示,六个面分别写有“祝”“福”“祖”“国”“万”“岁”,其中“祝”的对面是“祖”,“万”的对面是“岁”,则它的表面展开图可能是(　 　)

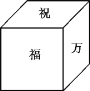
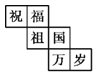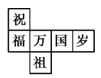    A. B. C. D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（14分）定义：底与腰的比是的等腰三角形叫做黄金等腰三角形．

    如图，已知△ABC中，AB=BC，∠C=36°，BA1平分∠ABC交AC于A1．

    （1）=AA1A C；

    （2）探究：△ABC是否为黄金等腰三角形？请说明理由；（提示：此处不妨设AC=1）

    （3）应用：已知AC=a，作A1B1∥AB交BC于B1，B1A2平分∠A1B1C交AC于A2，作A2B2∥AB交B2，B2A3平分∠A2B2C交AC于A3，作A3B3∥AB交BC于B3，…，依此规律操作下去，用含a，n的代数式表示An﹣1An．（n为大于1的整数，直接回答，不必说明理由）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】学校近期举办了一年一度的经典诵读比赛．某班级因节目需要，须购买A、B两种道具．已知购买1件A道具比购买1件B道具多10元，购买2件A道具和3件B道具共需要45元．

    （1）购买一件A道具和一件B道具各需要多少元？

    （2）根据班级情况，需要这两种道具共60件，且购买两种道具的总费用不超过620元．

    ①请问道具A最多购买多少件？

    ②若其中A道具购买的件数不少于B道具购买件数，该班级共有几种方案？试写出所有方案，并求出最少费用为多少元？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

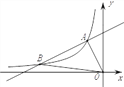
    【题目】如图，一次函数y＝k1x＋b的图象与反比例函数y＝ (x＜0)的图象相交于点A(－1，2)、点B(－4，n)．

    (1)求此一次函数和反比例函数的表达式；

    (2)求△AOB的面积；

    (3)在x轴上存在一点P，使△PAB的周长最小，求点P的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】4件同型号的产品中，有1件不合格品和3件合格品．

    （1）从这4件产品中随机抽取1件进行检测，求抽到的是不合格品的概率；

    （2）从这4件产品中随机抽取2件进行检测，求抽到的都是合格品的概率；

    （3）在这4件产品中加入x件合格品后，进行如下试验：随机抽取1件进行检测，然后放回，多次重复这个试验，通过大量重复试验后发现，抽到合格品的频率稳定在0.95，则可以推算出x的值大约是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，AB∥CD，∠ABK的角平分线BE的反向延长线和∠DCK的角平分线CF的反向延长线交于点H，∠K﹣∠H=27°，则∠K=（　　）

    A. 76° B. 78° C. 80° D. 82°

    查看答案和解析>>

    科目：初中数学 来源： 题型：

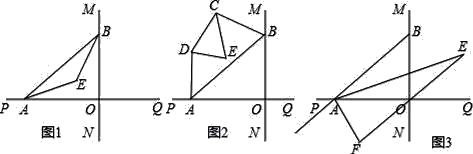
    【题目】直线MN与直线PQ垂直相交于O，点A在直线PQ上运动，点B在直线MN上运动．

    （1）如图1，已知AE、BE分别是∠BAO和∠ABO角的平分线，点A、B在运动的过程中，∠AEB的大小是否会发生变化？若发生变化，请说明变化的情况；若不发生变化，试求出∠AEB的大小．

    （2）如图2，已知AB不平行CD，AD、BC分别是∠BAP和∠ABM的角平分线，又DE、CE分别是∠ADC和∠BCD的角平分线，点A、B在运动的过程中，∠CED的大小是否会发生变化？若发生变化，请说明理由；若不发生变化，试求出其值．

    （3）如图3，延长BA至G，已知∠BAO、∠OAG的角平分线与∠BOQ的角平分线及延长线相交于E、F，在△AEF中，如果有一个角是另一个角的3倍，试求∠ABO的度数．

    查看答案和解析>>

    同步练习册答案