练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】商场出售的A型冰箱每台售价2190元，每日耗电量为1度，而B型节能冰箱每台售价虽比A型冰箱高出10%，但每日耗电量却为0.55度，现将A型冰箱打折出售，商场最少打几折消费者购买才合算？（按使用期为10年，每年365天，每度电0.40元计算）

    【答案】8折

    【解析】

    设商场最少打x折，消费者买才合算，先列出A冰箱10年的总费用2190×+10×365×0.4，再列出B冰箱10年的总费用1.1×2190+0.55×365×10×0.40，即可列方程求解.

    设商场最少打x折，消费者买才合算，由题意得

    2190×+10×365×0.4=1.1×2190+0.55×365×10×0.40，

    解得x=8

    答：设商场最少打8折，消费者买才合算.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】近年来市政府每年出资新建一批廉租房，使城镇住房困难的居民住房状况得到改善.下面是某小区2006～2008年每年人口总数和人均住房面积的统计的折线图(人均住房面积=该小区住房总面积/该小区人口总数，单位：㎡/人).

    根据以上信息，则下列说法：①该小区2006～2008年这三年中，2008年住房总面积最大；②该小区2007年住房总面积达到1.728×106 m；③该小区2008年人均住房面积的增长率为4%.其中正确的有

    （A）①②③（B）①②（C）① （D）③

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知，抛物线y=ax2﹣ax﹣4a与x轴交于A，B两点，与y轴交于C点，A点在B点左侧，C点在x轴下方，且△AOC∽△COB

    （1）求这条抛物线的解析式及直线BC的解析式；

    （2）设点D为抛物线对称轴上的一点，当点D在对称轴上运动时，是否可以与点C，A，B三点，构成梯形的四个顶点？若可以，求出点D坐标，若不可以，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，点O为直线AB上一点，过点O作射线OC，使∠BOC＝120°．将一直角三角形的直角顶点放在点O处，一边OM在射线OB上，另一边ON在直线AB的下方．

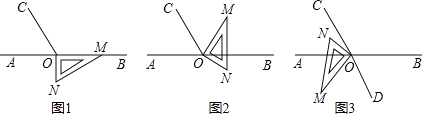
    （1）将图1中的三角板绕点O逆时针旋转至图2，使一边OM在∠BOC的内部，且恰好平分∠BOC，问：直线ON是否平分∠AOC？请说明理由；

    （2）将图1中的三角板绕点O按每秒5°的速度沿逆时针方向旋转一周，在旋转的过程中，第t秒时，直线ON恰好平分锐角∠AOC，则t的值为　 （直接写出结果）；

    （3）将图1中的三角板绕点O顺时针旋转至图3，使ON在∠AOC的内部，OD为∠BOM平分线．请探究：∠MOD与∠NOC之间的数量关系，并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

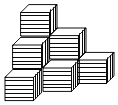
    【题目】棱长为a的正方体，摆放成如图所示的形状，动手试一试，并回答下列问题：

    （1）如果这一物体摆放了如图所示的上下三层，由几个正方体构成？

    （2）如图形所示物体的表面积是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在平面直角坐标系中，已知线段，点的坐标为，点的坐标为，如图1所示.

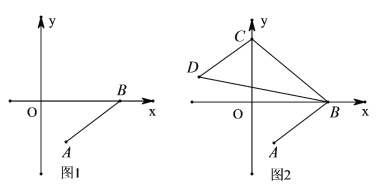
    (1)平移线段到线段，使点的对应点为，点的对应点为，若点的坐标为，求点的坐标；

    (2)平移线段到线段，使点在轴的正半轴上，点在第二象限内(与对应， 与对应)，连接如图2所示.若表示△BCD的面积)，求点、的坐标；

    (3)在(2)的条件下，在轴上是否存在一点，使？若存在，求出点的坐标,

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系xOy中，A、B为x轴上两点，C、D为y轴上的两点，经过点A、C、B的抛物线的一部分c1与经过点A、D、B的抛物线的一部分c2组合成一条封闭曲线，我们把这条封闭曲线成为“蛋线”．已知点C的坐标为（0，﹣ ），点M是抛物线C2：y=mx2﹣2mx﹣3m（m＜0）的顶点．

    （1）求A、B两点的坐标；

    （2）“蛋线”在第四象限上是否存在一点P，使得△PBC的面积最大？若存在，求出△PBC面积的最大值；若不存在，请说明理由；

    （3）当△BDM为直角三角形时，求m的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】【阅读学习】 刘老师提出这样一个问题：已知α为锐角，且tanα=，求sin2α的值．

    小娟是这样解决的：

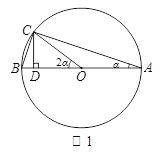
    如图1，在⊙O中，AB是直径，点C在⊙O上，∠BAC=α，所以∠ACB=90°，tanα==．

    易得∠BOC=2α．设BC=x，则AC=3x，则AB=x．作CD⊥AB于D，求出CD= （用含x的式子表示），可求得sin2α== ．

    【问题解决】

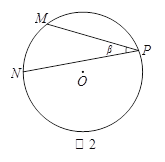
    已知，如图2，点M、N、P为圆O上的三点，且∠P=β，tanβ =，求sin2β的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

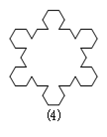
    【题目】如图，第（1）个多边形由正三角形“扩展”而来，边数记为a3，第（2）个多边形由正方形“扩展”而来，边数记为a4，……，依此类推，由正n边形“扩展”而来的多边形的边数记为an（n≥3）．则当an＝90时，n的值是_________．

    查看答案和解析>>

    同步练习册答案