
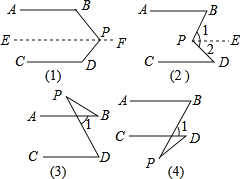
【题目】如图(1),AB∥CD,猜想∠BPD与∠B、∠D的关系,说出理由.
解:猜想∠BPD+∠B+∠D=360°
理由:过点P作EF∥AB,
∴∠B+∠BPE=180°(两直线平行,同旁内角互补)
∵AB∥CD,EF∥AB,
∴EF∥CD,(如果两条直线都和第三条直线平行,那么这两条直线也互相平行.)
∴∠EPD+∠D=180°(两直线平行,同旁内角互补)
∴∠B+∠BPE+∠EPD+∠D=360°
∴∠B+∠BPD+∠D=360°
(1)依照上面的解题方法,观察图(2),已知AB∥CD,猜想图中的∠BPD与∠B、∠D的关系,并说明理由.
(2)观察图(3)和(4),已知AB∥CD,猜想图中的∠BPD与∠B、∠D的关系,不需要说明理由.

【答案】见解析
【解析】
试题分析:(1)首先过点P作PE∥AB,由AB∥CD,可得PE∥AB∥CD,根据两直线平行,内错角相等,即可得∠1=∠B,∠2=∠D,则可求得∠BPD=∠B+∠D.
(2)由AB∥CD,根据两直线平行,内错角相等与三角形外角的性质,即可求得∠BPD与∠B、∠D的关系.
解:(1)∠BPD=∠B+∠D.
理由:如图2,过点P作PE∥AB,
∵AB∥CD,
∴PE∥AB∥CD,
∴∠1=∠B,∠2=∠D,
∴∠BPD=∠1+∠2=∠B+∠D;
(2)如图(3):∠BPD=∠D﹣∠B.
理由:∵AB∥CD,
∴∠1=∠D,
∵∠1=∠B+∠P,
∴∠D=∠B+∠P,
即∠BPD=∠D﹣∠B;
如图(4):∠BPD=∠B﹣∠D.
理由:∵AB∥CD,
∴∠1=∠B,
∵∠1=∠D+∠P,
∴∠B=∠D+∠P,
即∠BPD=∠B﹣∠D.


科目:初中数学 来源: 题型:
【题目】下列事件中,是确定事件的是( )
A. 打开电视机,它正在播放广告
B. 明天一定是天晴
C. 任意掷一枚质地均匀的骰子,掷出的点数是奇数
D. 抛出的篮球会下落
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市移动公司为了调查手机发送短信息的情况,在本区域的120位用户中抽取了10位用户来统计他们某周发信息的条数,结果如下表:
手机用户序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
发送短信息条数 | 20 | 19 | 20 | 20 | 21 | 17 | 15 | 23 | 20 | 25 |
本次调查中这120位用户大约每周一共发送条短信息.
查看答案和解析>>
科目:初中数学 来源: 题型:
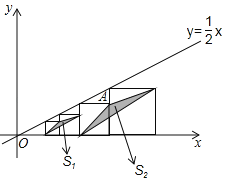
【题目】如图,在平面直角坐标系中,边长不等的正方形依次排列,每个正方形都有一个顶点落在函数y=![]() x的图象上,从左向右第3个正方形中的一个顶点A的坐标为(6,2),阴影三角形部分的面积从左向右依次记为S1、S2、S3、…、Sn,则第4个正方形的边长是 ,S3的值为 .
x的图象上,从左向右第3个正方形中的一个顶点A的坐标为(6,2),阴影三角形部分的面积从左向右依次记为S1、S2、S3、…、Sn,则第4个正方形的边长是 ,S3的值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
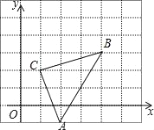
【题目】如图,直角坐标系中,△ABC的顶点都在网格点上,其中,C点坐标为(1,2)
(1)写出点A、B的坐标:A( , )、B( , )
(2)将△ABC先向左平移1个单位长度,再向上平移2个单位长度,得到△A′B′C′,画出△A′B′C′
(3)写出三个顶点坐标A′( 、 )、B′( 、 )、C′ ( 、 )
(4)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先化简,再求值:
(1)(x+2)2-(x+5)(x-5),其中x=![]() 。
。
(2)[(x+2y)2-(x+y)(3x-y)-5y2]÷2x,其中x=-2,y=![]() 。
。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线经过![]() ,
,![]()
![]() ,⊙M是△ABC的外接圆,M为圆心.
,⊙M是△ABC的外接圆,M为圆心.
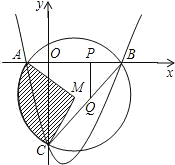
(1)求抛物线的解析式;
(2)求阴影部分的面积;
(3)在正半轴上有一点P,作PQ⊥x轴交BC于Q,设PQ=k,△CPQ的面积为S,求S关于k的函数关系式,并求出S的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com