
(本题满分10分)如图,⊙O是△ABC的外接圆,AB是⊙O的直径,D为⊙O上一点,OD⊥AC,垂足为E,连接BD.

(1)求证:BD平分∠ABC;
(2) 当∠ODB=30°时,求证:BC=OD.
【解析】
试题分析:(1)由OD⊥AC ,OD为半径,根据垂径定理,即可得 =
= ,又由在同圆或等圆中,同弧或等弧所对的圆周角相等,即可证得BD平分∠ABC;
,又由在同圆或等圆中,同弧或等弧所对的圆周角相等,即可证得BD平分∠ABC;
(2)首先由OB=OD,易求得∠AOD的度数,又由OD⊥AC于E,可求得∠A的度数,然后由AB是⊙O的直径,根据圆周角定理,可得∠ACB=90°,继而可证得BC=OD.
试题解析:(1)∵OD⊥AC OD为半径,
∴  =
= .
.
∴∠CBD=∠ABD。
∴BD平分∠ABC.
(2)∵OB=OD,∠ODB=30°,
∴∠OBD=∠ODB=30°.
∴∠AOD=∠OBD+∠ODB=30°+30°=60°.
又∵OD⊥AC于E,
∴∠OEA=90°.
∴∠A=180°-∠OEA-∠AOD=180°-90°-60°=30°.
又∵AB为⊙O的直径,
∴∠ACB=90°.
∴在Rt△ACB中,BC= AB .
AB .
∵OD= AB,
AB,
∴BC=OD.
考点:垂径定理, 圆周角定理


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:初中数学 来源:2014-2015学年广东省八年级上学期期中数学试卷(解析版) 题型:选择题
点A(—3,4)关于x轴对称的点的坐标是( )
A.(3,—4) B.(—3,—4) C.(3,4) D.(—4,—3)
查看答案和解析>>
科目:初中数学 来源:2014-2015学年广东省广州市九年级上学期期中考试数学试卷(解析版) 题型:解答题
(本题满分14分)如图1,四边形ABCD是边长为 的正方形,长方形AEFG的宽
的正方形,长方形AEFG的宽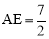 ,长
,长 .将长方形AEFG绕点A顺时针旋转15°得到长方形AMNH (如图2),这时BD与MN相交于点O.
.将长方形AEFG绕点A顺时针旋转15°得到长方形AMNH (如图2),这时BD与MN相交于点O.

(1)求 的度数;
的度数;
(2)在图2中,求D、N两点间的距离;
(3)若把长方形AMNH绕点A再顺时针旋转15°得到长方形ARTZ,请问此时点B在矩形ARTZ的
内部、外部、还是边上?并说明理由.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年广东省广州市九年级上学期期中考试数学试卷(解析版) 题型:填空题
如图,直角梯形ABCD中,AD//BC,AB⊥BC,AD=3,BC=5,将腰DC绕点D逆时针方向旋转90°至DE,连接AE,则△ADE的面积是_________

查看答案和解析>>
科目:初中数学 来源:2014-2015学年广东省广州市九年级上学期期中考试数学试卷(解析版) 题型:选择题
如图, 是等腰直角三角形,
是等腰直角三角形, 是斜边,将
是斜边,将 绕点
绕点 逆时针旋转后,能与
逆时针旋转后,能与 重合,如果
重合,如果 ,那么
,那么 的长等于( )
的长等于( )

(A) (B)
(B) (C)
(C) (D)
(D)
查看答案和解析>>
科目:初中数学 来源:2014-2015学年广东省广州市九年级上学期综合测试一数学试卷(解析版) 题型:填空题
如图,将边长为12的正方形ABCD沿其对角线AC剪开,再把△ABC沿着AD方向平移,得到△ ,当两个三角形重叠的面积为32时,它移动的距离
,当两个三角形重叠的面积为32时,它移动的距离 等于 .
等于 .

查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省江阴市长泾片九年级上学期期中考试数学试卷(解析版) 题型:填空题
如图,点A、B、C在⊙O上,AB∥CO,∠B=22º,则∠A= º.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com