
(本题满分14分)如图1,四边形ABCD是边长为 的正方形,长方形AEFG的宽
的正方形,长方形AEFG的宽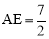 ,长
,长 .将长方形AEFG绕点A顺时针旋转15°得到长方形AMNH (如图2),这时BD与MN相交于点O.
.将长方形AEFG绕点A顺时针旋转15°得到长方形AMNH (如图2),这时BD与MN相交于点O.

(1)求 的度数;
的度数;
(2)在图2中,求D、N两点间的距离;
(3)若把长方形AMNH绕点A再顺时针旋转15°得到长方形ARTZ,请问此时点B在矩形ARTZ的
内部、外部、还是边上?并说明理由.
(1)∠DOM=120°(2)DN=5(3)点B在矩形ARTZ的外部
【解析】
试题分析:(1)由旋转的性质,可得∠BAM=15°,即可得∠OKB=∠AOM=75°,又由正方形的性质,可得
∠ABD=45°,然后利用外角的性质,即可求得∠DOM的度数;
(2)首先连接AM,交BD于I,连接AN,由特殊角的三角函数值,求得∠HAN=30°,又由旋转的性质,即可求得∠DAN=45°,即可证得A,C,N共线,然后由勾股定理求得答案;
(3)在Rt△ARK中,利用三角函数即可求得AK的值,与AB比较大小,即可确定B的位置.
试题解析:(1)如图,设AB与MN相交于点K,根据题意得:∠BAM=15°,
∵四边形AMNH是矩形,∴∠M=90°.
∴∠AKM=90°-∠BAM=75°.
∴∠BKO=∠AKM=75°.
∵四边形ABCD是正方形,∴∠ABD=45°.
∴∠DOM=∠BKO+?ABD=75°+45°=120°.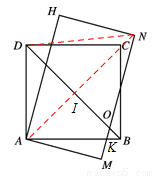
(2)连接AN,交BD于I,连接DN,
∵NH= ,AH=
,AH=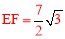 ,∠H=90°,
,∠H=90°,
∴ 。∴∠HAN=30°.
。∴∠HAN=30°.
∴AN=2NH=7.
由旋转的性质:∠DAH=15°,∴∠DAN=45°.
∵∠DAC=45°,∴A,C,N共线.
∵四边形ABCD是正方形,∴BD⊥AC.
∵AD=CD=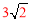 ,∴
,∴
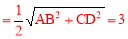 .
.
∴NI=AN-AI=7-3=4.
在Rt△DIN中, .
.
(3)点B在矩形ARTZ的外部.理由如下:
如图,根据题意得:∠BAR=15°+15°=30°.
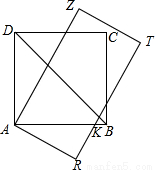
∵∠R=90°,AR=  ,
,
∴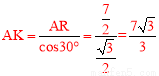 。
。
∵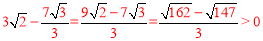 ,
,
∴AB=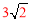 >
>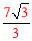 .
.
∴点B在矩形ARTZ的外部.
考点:旋转的性质,正方形的性质, 外角的性质, 特殊角的三角函数值,勾股定理


 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案科目:初中数学 来源:2014-2015学年广东省汕头市九年级上学期第一次阶段质量检测数学试卷(解析版) 题型:解答题
已知某抛物线的顶点为(1,3),且过点(3,0),求此抛物线的解析式.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年广东省汕头市七年级上学期期中考试数学试卷(解析版) 题型:选择题
计算3a-2a的结果正确的是( )
A、1 B、a C、-a D、-5a
查看答案和解析>>
科目:初中数学 来源:2014-2015学年广东省广州市九年级上学期期中考试数学试卷(解析版) 题型:解答题
(本题满分10分)如图,⊙O是△ABC的外接圆,AB是⊙O的直径,D为⊙O上一点,OD⊥AC,垂足为E,连接BD.

(1)求证:BD平分∠ABC;
(2) 当∠ODB=30°时,求证:BC=OD.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年广东省广州市九年级上学期期中考试数学试卷(解析版) 题型:填空题
如图,已知⊙O是△ABD的外接圆,AB是⊙O的直径,CD是⊙O的弦,∠ABD=58°,则∠BCD等于_________________

查看答案和解析>>
科目:初中数学 来源:2014-2015学年广东省广州市九年级上学期综合测试一数学试卷(解析版) 题型:解答题
已知一次函数 的图象如图所示.
的图象如图所示.
(1)求该一次函数的解析式;
(2)直接写出:当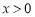 时,
时, 的取值范围
的取值范围

查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省江阴市长泾片九年级上学期期中考试数学试卷(解析版) 题型:解答题
解下列方程(每小题3分,共9分)
(1)
(2)(x+3)2=2x+5
(3)(2x+1)(x-3)=-4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com