
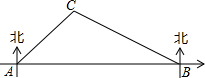
 如图,在合肥市轨道交通建设中,规划在A、B两地修建一段地铁,点B在点A的正东方向,由于A、B之间建筑物较多,无法直接测量,现选参照物C,测得C在点A的东北方向上,在点B的北偏西60°方向上,B、C两点间距离为800m.请你求出这段地铁AB的长度.(结果精确到1m,参考数据:$\sqrt{2}$≈1.414,≈1.732)
如图,在合肥市轨道交通建设中,规划在A、B两地修建一段地铁,点B在点A的正东方向,由于A、B之间建筑物较多,无法直接测量,现选参照物C,测得C在点A的东北方向上,在点B的北偏西60°方向上,B、C两点间距离为800m.请你求出这段地铁AB的长度.(结果精确到1m,参考数据:$\sqrt{2}$≈1.414,≈1.732) 科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{2+3}$=$\sqrt{2}$+$\sqrt{3}$ | B. | (-$\sqrt{3}$)2=3 | C. | 3a-a=3 | D. | (a2)3=a5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x≥0 | B. | x>-2 | C. | -2<x≤3 | D. | x≤3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com