
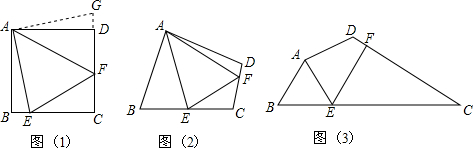
分析 (1)根据旋转变换的性质和正方形的性质证明△EAF≌△GAF,得到EF=FG,证明结论;
(2)把△ABE绕点A逆时针旋转至△ADH,使AB与AD重合,证明△EAF≌△HAF,证明即可;
(3)延长BA交CD的延长线于P,连接AF,根据四边形内角和定理求出∠C的度数,得到∠P=90°,求出PD、PA,证明∠EAF=$\frac{1}{2}$∠BAD,又(2)的结论得到答案.
解答 (1)证明:由旋转的性质可知,△ABE≌△ADG,
∴BE=DG,AE=AG,∠BAE=∠DAG,∠ADG=∠ABE=90°,
∴G、D、F在同一条直线上,
∵四边形ABCD是正方形,
∴∠BAD=90°,
∴∠EAG=90°,又∠EAF=45°,
∴∠FAG=45°,
在△EAF和△GAF中,
$\left\{\begin{array}{l}{AE=AG}\\{∠EAF=∠GAF}\\{AF=AF}\end{array}\right.$,
∴△EAF≌△GAF,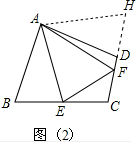
∴EF=FG,
∴EF=BE+FD;
(2)当∠EAF=$\frac{1}{2}$∠BAD时,仍有EF=BE+FD.
证明:如图(2),把△ABE绕点A逆时针旋转至△ADH,使AB与AD重合,
则BE=DH,∠BAE=∠DAH,∠ADH=∠B,又∠B+∠D=180°,
∴∠ADH+∠D=180°,即F、D、H在同一条直线上,
当∠EAF=$\frac{1}{2}$∠BAD时,∠EAF=∠HAF,
由(1)得,△EAF≌△HAF,
则EF=FH,即EF=BE+FD,
故答案为:∠EAF=$\frac{1}{2}$∠BAD;
(3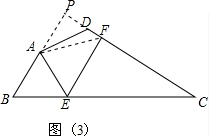 )如图(3),延长BA交CD的延长线于P,连接AF,
)如图(3),延长BA交CD的延长线于P,连接AF,
∵∠B=60°,∠ADC=120°,∠BAD=150°,
∴∠C=30°,
∴∠P=90°,又∠ADC=120°,
∴∠ADP=60°,
∴PD=AD×cos∠ADP=40,AP=AD×sin∠ADP=40$\sqrt{3}$,
∴PF=PD+DF=40$\sqrt{3}$,
∴PA=PF,
∴∠PAF=45°,又∠PAD=30°,
∴∠DAF=15°,
∴∠EAF=75°,∠BAE=60°,
∴∠EAF=$\frac{1}{2}$∠BAD,
由(2)得,EF=BE+FD,又BE=BA=80,
∴EF=BE+FD=40($\sqrt{3}+1$).
点评 本题考查的是正方形的性质、旋转变换的性质、全等三角形的判定和性质,掌握正方形的四条边都相等、四个角都是直角,旋转变换的旋转角相等、旋转后的三角形与原三角形全等是解题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
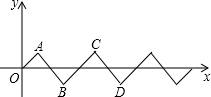 如图,在平面直角坐标系中,将斜边长为2个等腰直角三角形按如图所示的位置摆放,得到一条折线O-A-B-C-D…,点P从点O出发沿着折线以每秒$\sqrt{2}$的速度向右运动,2016秒时,点P的坐标是(2016,0).
如图,在平面直角坐标系中,将斜边长为2个等腰直角三角形按如图所示的位置摆放,得到一条折线O-A-B-C-D…,点P从点O出发沿着折线以每秒$\sqrt{2}$的速度向右运动,2016秒时,点P的坐标是(2016,0).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
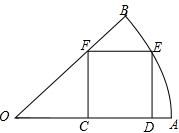 如图,在圆心角为45°的扇形内有一正方形CDEF,其中点C、D在半径OA上,点F在半径OB上,点E在$\widehat{AB}$上,则扇形与正方形的面积比是( )
如图,在圆心角为45°的扇形内有一正方形CDEF,其中点C、D在半径OA上,点F在半径OB上,点E在$\widehat{AB}$上,则扇形与正方形的面积比是( )| A. | π:8 | B. | 5π:8 | C. | $\sqrt{3}$π:4 | D. | $\sqrt{5}$π:4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
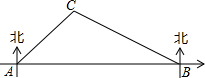 如图,在合肥市轨道交通建设中,规划在A、B两地修建一段地铁,点B在点A的正东方向,由于A、B之间建筑物较多,无法直接测量,现选参照物C,测得C在点A的东北方向上,在点B的北偏西60°方向上,B、C两点间距离为800m.请你求出这段地铁AB的长度.(结果精确到1m,参考数据:$\sqrt{2}$≈1.414,≈1.732)
如图,在合肥市轨道交通建设中,规划在A、B两地修建一段地铁,点B在点A的正东方向,由于A、B之间建筑物较多,无法直接测量,现选参照物C,测得C在点A的东北方向上,在点B的北偏西60°方向上,B、C两点间距离为800m.请你求出这段地铁AB的长度.(结果精确到1m,参考数据:$\sqrt{2}$≈1.414,≈1.732)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a2•a2=a4 | B. | (a-b)2=a2-b2 | C. | 2+$\sqrt{2}$=2$\sqrt{2}$ | D. | (-a3)2=-a6 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2(x+y)=2x+y | B. | 2a(a+b)=2a2+b | ||
| C. | 10ab÷(-5a)=-2 | D. | (x-a)(x-b)=x2-(a+b)x+ab |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com