
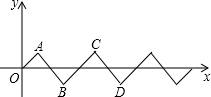
 如图,在平面直角坐标系中,将斜边长为2个等腰直角三角形按如图所示的位置摆放,得到一条折线O-A-B-C-D…,点P从点O出发沿着折线以每秒$\sqrt{2}$的速度向右运动,2016秒时,点P的坐标是(2016,0).
如图,在平面直角坐标系中,将斜边长为2个等腰直角三角形按如图所示的位置摆放,得到一条折线O-A-B-C-D…,点P从点O出发沿着折线以每秒$\sqrt{2}$的速度向右运动,2016秒时,点P的坐标是(2016,0). 分析 根据图象可得移动4次图象完成一个循环,从而可得出点A2016的坐标.
解答 解:因为等腰直角三角形,点P从点O出发沿着折线以每秒$\sqrt{2}$的速度向右运动,可得:
当点P从原点O出发,沿这条曲线向右运动,运动时间为1秒时,点A的坐标为(1,1),
当点P从原点O出发,沿这条曲线向右运动,运动时间为2秒时,点的坐标为(2,0),
当点P从原点O出发,沿这条曲线向右运动,运动时间为3秒时,点B的坐标为(3,-1),
当点P从原点O出发,沿这条曲线向右运动,运动时间为4秒时,点的坐标为(4,0),
当点P从原点O出发,沿这条曲线向右运动,运动时间为5秒时,点C的坐标为(5,1),
当点P从原点O出发,沿这条曲线向右运动,运动时间为6秒时,点的坐标为(6,0),
…,
∵2016÷4=504,
∴A2016的坐标是(2016,0),
故答案为:(2016,0).
点评 此题考查了点的规律变化,解答本题的关键是仔细观察图象,得到点的变化规律,解决问题.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:选择题
 已知二次函数y=ax2+bx=c(a≠0)的图象如图所示,与y轴相交一点C,与x轴负半轴相交一点A,且OA=OC,有下列5个结论:
已知二次函数y=ax2+bx=c(a≠0)的图象如图所示,与y轴相交一点C,与x轴负半轴相交一点A,且OA=OC,有下列5个结论:| A. | ③④⑤ | B. | ③④ | C. | ①②③ | D. | ②③④ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{2+3}$=$\sqrt{2}$+$\sqrt{3}$ | B. | (-$\sqrt{3}$)2=3 | C. | 3a-a=3 | D. | (a2)3=a5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com