
 已知二次函数y=ax2+bx=c(a≠0)的图象如图所示,与y轴相交一点C,与x轴负半轴相交一点A,且OA=OC,有下列5个结论:
已知二次函数y=ax2+bx=c(a≠0)的图象如图所示,与y轴相交一点C,与x轴负半轴相交一点A,且OA=OC,有下列5个结论:| A. | ③④⑤ | B. | ③④ | C. | ①②③ | D. | ②③④ |
分析 由抛物线的开口方向判断a与0的关系,由抛物线与y轴的交点判断c与0的关系,然后根据对称轴及抛物线与x轴交点情况进行推理,进而对所得结论进行判断.
解答 解:由抛物线的开口方向向下可推出a<0;
因为对称轴在y轴右侧,对称轴为x=-$\frac{b}{2a}$>0,又因为a<0,∴b>0;
由抛物线与y轴的交点在y轴的正半轴上,
∴c>0故abc<0,①错误;
当x=-1时,y<0,∴a-b+c<0,即b>a+c,②错误;
当x=2时,y>0,∴4a+2b+c>0,③正确;
由图象可知:对称轴x=-$\frac{b}{2a}$=1,
∴2a+b=0,④正确;
由图象可知:OC=|c|=c (∵c>0),
∵OA=OC,
∴OA=OC=|c|.
则A点的坐标为(-c,0),代入函数解析式可得ac2-bc+c=0,
化简得ac-b+1=0,c+$\frac{1}{a}$=$\frac{b}{a}$,
又∵-$\frac{b}{2a}$=1,
∴$\frac{b}{a}$=-2,故c+$\frac{1}{a}$=-2,⑤正确.
∴③④⑤正确,
故选A.
点评 本题考查了二次函数图象与系数的关系,主要利用图象求出a,b,c的范围,以及特殊值的代入能得到特殊的式子.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:选择题
| A. | 8.5×109 | B. | 8.5×1010 | C. | 8.5×1011 | D. | 8.5×1012 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (a+b)2=a2+b2 | B. | $\sqrt{a^2+b^2}$=$\sqrt{a^2}$+$\sqrt{b^2}$ | C. | a2•a3=a5 | D. | $\sqrt{{a}^{4}}$=±a2 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
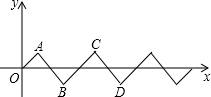 如图,在平面直角坐标系中,将斜边长为2个等腰直角三角形按如图所示的位置摆放,得到一条折线O-A-B-C-D…,点P从点O出发沿着折线以每秒$\sqrt{2}$的速度向右运动,2016秒时,点P的坐标是(2016,0).
如图,在平面直角坐标系中,将斜边长为2个等腰直角三角形按如图所示的位置摆放,得到一条折线O-A-B-C-D…,点P从点O出发沿着折线以每秒$\sqrt{2}$的速度向右运动,2016秒时,点P的坐标是(2016,0).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
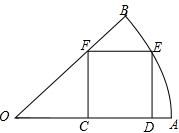 如图,在圆心角为45°的扇形内有一正方形CDEF,其中点C、D在半径OA上,点F在半径OB上,点E在$\widehat{AB}$上,则扇形与正方形的面积比是( )
如图,在圆心角为45°的扇形内有一正方形CDEF,其中点C、D在半径OA上,点F在半径OB上,点E在$\widehat{AB}$上,则扇形与正方形的面积比是( )| A. | π:8 | B. | 5π:8 | C. | $\sqrt{3}$π:4 | D. | $\sqrt{5}$π:4 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2(x+y)=2x+y | B. | 2a(a+b)=2a2+b | ||
| C. | 10ab÷(-5a)=-2 | D. | (x-a)(x-b)=x2-(a+b)x+ab |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com