
分析 将原式利用完全平方公式配方成$\frac{1}{2}$[(a+b)2+(b+c)2+(a-c)2],根据已知条件相减可得a-c=4,将a+b、b+c、a-c代入计算可得.
解答 解:∵a+b=2+$\sqrt{3}$,b+c=2-$\sqrt{3}$,
∴a-c=4,
则a2+b2+c2+ab+bc-ca=$\frac{1}{2}$(a2+2ab+b2+b2+2bc+c2+a2-2ac+c2)
=$\frac{1}{2}$[(a+b)2+(b+c)2+(a-c)2]
=$\frac{1}{2}$[(2+$\sqrt{3}$)2+(2$-\sqrt{3}$)2+42]
=$\frac{1}{2}$×(4+4$\sqrt{3}$+3+4-4$\sqrt{3}$+3+16)
=$\frac{1}{2}$×30
=15.
点评 本题主要考查因式分解的应用,熟练掌握完全平方公式是解题的根本,灵活运用是解决本题的关键.


科目:初中数学 来源: 题型:解答题
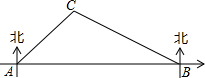 如图,在合肥市轨道交通建设中,规划在A、B两地修建一段地铁,点B在点A的正东方向,由于A、B之间建筑物较多,无法直接测量,现选参照物C,测得C在点A的东北方向上,在点B的北偏西60°方向上,B、C两点间距离为800m.请你求出这段地铁AB的长度.(结果精确到1m,参考数据:$\sqrt{2}$≈1.414,≈1.732)
如图,在合肥市轨道交通建设中,规划在A、B两地修建一段地铁,点B在点A的正东方向,由于A、B之间建筑物较多,无法直接测量,现选参照物C,测得C在点A的东北方向上,在点B的北偏西60°方向上,B、C两点间距离为800m.请你求出这段地铁AB的长度.(结果精确到1m,参考数据:$\sqrt{2}$≈1.414,≈1.732)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| L1/m | 0.2 | 0.4 | 0.6 | 0.8 | 1 | 1.2 |
| F1/N | 12 | 6 | 4 | 3 | 2.4 | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | A+B=0 | B. | A=B | C. | AB=0 | D. | A=2B |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 有一条长40m的篱笆,现借用一堵墙(笔直的、充分长)将篱笆围成一个四边形鸡场.
有一条长40m的篱笆,现借用一堵墙(笔直的、充分长)将篱笆围成一个四边形鸡场.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com