
 有一条长40m的篱笆,现借用一堵墙(笔直的、充分长)将篱笆围成一个四边形鸡场.
有一条长40m的篱笆,现借用一堵墙(笔直的、充分长)将篱笆围成一个四边形鸡场.分析 (1)设长方形鸡场的宽AB=xm,则长BC=(40-2x)m,鸡场的面积为ym2,根据长乘以宽等于面积列出函数关系式,配方可得最值情况;
(2)可充分利用篱笆后面的一堵墙来扩展四边形的面积作为切入点.
解答 解:(1)设长方形鸡场的宽AB=xm,则长BC=(40-2x)m,鸡场的面积为ym2,
根据题意,得:y=x(40-2x)=-2x2+40x=-2(x-10)2+200,
故当x=10时,y取得最大值200,
答:当长方形的长为20m,宽为10米时,养鸡场的面积最大,最大面积为200m2;
(2)如果将图1中的点A、D分别向外移动.
那么ABCD仍然是四边形,而将四边形沿墙反射过来,这样就得到一个新的封闭六边形BCDC′B′A,它的周长等于原篱笆长度的两倍.
所以当六边形BCDC′B′A为正六边形,
即AB=BC=CD,且∠BAD=∠CDA=60°,∠ABC=∠DCB=120°时,六边形BCDC′B′A的面积最大.
因而其一半即四边形ABCD的面积也最大.由于周长相等,
因此图中正六边形BCDC′B′A的面积大于(1)中长方形面积,
所以图中四边形ABCD的面积大于(1)中四边形ABCD的面积.
点评 本题主要考查二次函数的实际应用能力,根据相等关系列函数关系式并求最大值是解题的根本,利用墙的长度来扩展四边形的面积是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3 | B. | 2或-4 | C. | 2 | D. | 3或-1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
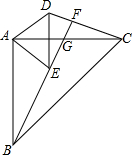 如图,已知AB=AC,AD=AE,∠BAC=90°,∠EAD=90°,BE的延长线交AC于G,交CD于F.
如图,已知AB=AC,AD=AE,∠BAC=90°,∠EAD=90°,BE的延长线交AC于G,交CD于F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com