
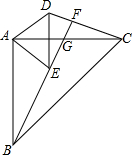
 如图,已知AB=AC,AD=AE,∠BAC=90°,∠EAD=90°,BE的延长线交AC于G,交CD于F.
如图,已知AB=AC,AD=AE,∠BAC=90°,∠EAD=90°,BE的延长线交AC于G,交CD于F.分析 (1)利用全等三角形的性质和判定,以及直角三角形的判断方法,从而得到∠BFC=90°,即得出结论.
(2)利用角平分线的定义和垂直平分线的性质和判断方法,得出∠ABE=∠ACD=22.5°,再利用三角形的一个外角等于与它不相邻的两内角之和,从而得出∠DGF=45°,最后利用等腰直角三角形的特点得出DG=$\sqrt{2}$FG.
解答 证明:(1)∵∠BAE+∠CAE=∠BAC=90°
∠DAC+∠CAE=∠DAE=90°
∵∠BAE=∠DAC(同角的余角相等)
∵AB=AC,AE=AD
∴△ABE≌△ACD(SAS)
∴∠ABE=∠ACD,
∵∠ABE+∠AGB=90°,
∴∠ACD+∠AGB=90°
∵∠AGB=∠CGF(对顶角相等),
∴∠ACD+∠CGF=90°,
∴BF⊥CD 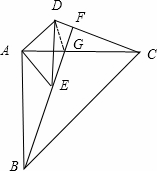
(2)连接DG
∵AE平分∠BAC,
∴∠BAE=∠CAE,
∵∠BAE=∠DAC,
∴∠CAE=∠DAE,
∵AD=AE,
∴AG垂直平分DE,
∴EG=DG(垂直平分线上的点到两端的距离相等)
∵BF平分∠ABC,
∴∠ABE=$\frac{1}{2}$∠ABC=$\frac{1}{2}$×45°=22.5°,
∵∠ABE=∠ACD,
∴∠ACD=22.5°
∵AB⊥AC,DE⊥AC,
∴AB∥DE,
∴∠ABE=∠DEF=22.5°
∵EG=DG,
∴∠DEF=∠EDG=22.5°,
∴∠FDG=90°-∠ACD-∠EDG=90°-22.5°-22.5°=45°,
∵∠FGD=∠EDG+DEG=22.5°+22.5°=45°,
∴∠FDG=∠FGD=45°,
∵∠DFG=90°,
∴DG=$\sqrt{2}$FG,
∴EG=DG=$\sqrt{2}$FG.
点评 本题主要考查了等腰直角三角形的性质,证明垂直的方法,三角形的角平分线的性质以及垂直平分线的性质和判断方法.


 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案科目:初中数学 来源: 题型:填空题
| L1/m | 0.2 | 0.4 | 0.6 | 0.8 | 1 | 1.2 |
| F1/N | 12 | 6 | 4 | 3 | 2.4 | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 有一条长40m的篱笆,现借用一堵墙(笔直的、充分长)将篱笆围成一个四边形鸡场.
有一条长40m的篱笆,现借用一堵墙(笔直的、充分长)将篱笆围成一个四边形鸡场.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 已知实数a,b,c在数轴上的位置如图所示,且|a|=|b|,化简:|a|+|a+b|-$\sqrt{(c-a)^{2}}$-2$\sqrt{{c}^{2}}$=3c-2a.
已知实数a,b,c在数轴上的位置如图所示,且|a|=|b|,化简:|a|+|a+b|-$\sqrt{(c-a)^{2}}$-2$\sqrt{{c}^{2}}$=3c-2a.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com