
 已知实数a,b,c在数轴上的位置如图所示,且|a|=|b|,化简:|a|+|a+b|-$\sqrt{(c-a)^{2}}$-2$\sqrt{{c}^{2}}$=3c-2a.
已知实数a,b,c在数轴上的位置如图所示,且|a|=|b|,化简:|a|+|a+b|-$\sqrt{(c-a)^{2}}$-2$\sqrt{{c}^{2}}$=3c-2a. 科目:初中数学 来源: 题型:选择题
| A. | 3 | B. | 2或-4 | C. | 2 | D. | 3或-1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
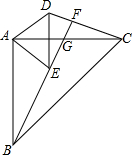 如图,已知AB=AC,AD=AE,∠BAC=90°,∠EAD=90°,BE的延长线交AC于G,交CD于F.
如图,已知AB=AC,AD=AE,∠BAC=90°,∠EAD=90°,BE的延长线交AC于G,交CD于F.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
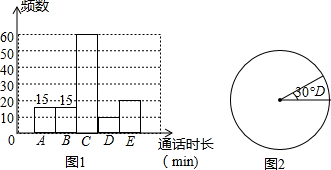 现如今,收集已成为人们普遍的交流工具,人们用它来打电话、上网.为了解3月份某单位职工的本地通话时长,随机抽取了该单位职工的通话时长进行抽样调查,将调查结果分成为A,B,C,D五个组,并利用所得数据绘制了如图1所示的频数分布直方图和如图2所示的不完整的扇形统计图.
现如今,收集已成为人们普遍的交流工具,人们用它来打电话、上网.为了解3月份某单位职工的本地通话时长,随机抽取了该单位职工的通话时长进行抽样调查,将调查结果分成为A,B,C,D五个组,并利用所得数据绘制了如图1所示的频数分布直方图和如图2所示的不完整的扇形统计图. | 组别 | 通话时长(min) |
| A | x<100 |
| B | 100≤x<200 |
| C | 200≤x<300 |
| D | 300≤x<400 |
| E | x>400 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
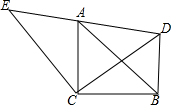 如图,△ACB和△ECD都是等腰直角三角形,CA=CB,CE=CD,△ACB的顶点A在△ECD的斜边上,连接BD.
如图,△ACB和△ECD都是等腰直角三角形,CA=CB,CE=CD,△ACB的顶点A在△ECD的斜边上,连接BD.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com