
【题目】如图,点O为等边三角形ABC内一点,连接OA,OB,OC,以OB为一边作∠OBM=60°,且BO=BM,连接CM,OM.
(1)判断AO与CM的大小关系并证明;
(2)若OA=8,OC=6,OB=10,判断△OMC的形状并证明.
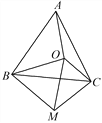
【答案】(1)AO=CM (2)△OMC是直角三角形
【解析】试题分析:(1)先证明△OBM是等边三角形,得出OM=OB,∠ABC=∠OBC,由SAS证明△AOB≌△CMB,即可得出结论;
(2)由勾股定理的逆定理即可得出结论.
试题解析:解:(1)AO=CM.理由如下:
∵∠OBM=60°,OB=BM,∴△OBM是等边三角形,∴OM=OB=10,∠ABC=∠OBC=60°,
∴∠ABO=∠CBM.在△AOB和△CMB中,∵OB=OM,∠ABO=∠CBM,AB=BC,∴△AOB≌△CMB(SAS),∴OA=MC;
(2)△OMC是直角三角形;理由如下:
在△OMC中,OM2=100,OC2+CM2=62+82=100,∴OM2=OC2+CM2,∴△OMC是直角三角形.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】关于频率与概率有下列几种说法:
①“明天下雨的概率是 90%”表示明天下雨的可能性很大;
②“抛一枚硬币正面朝上的概率为”表示每抛两次就有一次正面朝上;
③“某彩票中奖的概率是 1%”表示买 10 张该种彩票不可能中奖;
④“抛一枚硬币正面朝上的概率为![]() ”表示随着抛掷次数的增加,“抛出正面朝上”这一事件发生的频率稳定在
”表示随着抛掷次数的增加,“抛出正面朝上”这一事件发生的频率稳定在![]() 附近.
附近.
正确的说法是( )
A. ①③ B. ①④ C. ②③ D. ②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,A(-2,0) ,B(-1,2) ,C(1,0) ,连接 AB,点 D 为 AB 的中点,连接 OB 交 CD于点 E,则四边形 DAOE 的面积为( )
A. 1. B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正比例函数y=2x和反比例函数的图象交于点A(m,﹣2).
(1)求反比例函数的解析式;
(2)观察图象,直接写出正比例函数值大于反比例函数值时自变量x的取值范围;
(3)若双曲线上点C(2,n)沿OA方向平移 ![]() 个单位长度得到点B,判断四边形OABC的形状并证明你的结论.
个单位长度得到点B,判断四边形OABC的形状并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2017年5月,某县突降暴雨,造成山体滑坡,桥梁垮塌,房屋大面积受损,该省民政厅急需将一批帐篷送往灾区.现有甲、乙两种货车,已知甲种货车比乙种货车每辆车多装20件帐篷,且甲种货车装运1 000件帐篷与乙种货车装运800件帐篷所用车辆相等.
(1)求甲、乙两种货车每辆车可装多少件帐篷;
(2)如果这批帐篷有1 490件,用甲、乙两种汽车共16辆装运,甲种车辆刚好装满,乙种车辆最后一辆只装了50件,其余装满,求甲、乙两种货车各有多少辆.
查看答案和解析>>
科目:初中数学 来源: 题型:
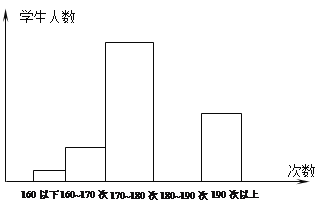
【题目】为了解中学生的体能情况,某校抽取了50名八年级学生进行一分钟跳绳次数测试,将所得数据整理后,画出了频数分布直方图如下图所示已知图中从左到右前第一、第二、第三、第五小组的频率分别为0.04 , 0.12 ,0.4 ,O.28 ,根据已知条件解答下列问题:
(1)第四个小组的频率是多少? 你是怎样得到的?
(2)这五小组的频数各是多少?
(3)在这次跳绳中,跳绳次数的中位数落在第几小组内?
(4)将频数分布直方图补全,并分别写出各个小组的频数,并画出频数分布折线图.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在数轴上有三个点A,B,C,回答下列问题:
(1)若将点B向右移动6个单位后,三个点所表示的数中最小的数是多少?
(2)在数轴上找一点D,使点D到A,C两点的距离相等,写出点D表示的数;
(3)在点B左侧找一点E,使点E到点A的距离是到点B的距离的2倍,并写出点E表示的数.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+c(b>a>0)与x轴最多有一个交点,现有以下四个结论:
①该抛物线的对称轴在y轴左侧;
②关于x的方程ax2+bx+c+2=0无实数根;
③a﹣b+c≥0;
④ ![]() 的最小值为3.
的最小值为3.
其中,正确结论的个数为( )
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com