
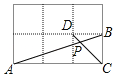
【题目】如图,在边长相同的小正方形网格中,点A、B、C、D都在这些小正方形的顶点上,AB与CD相交于点P,则tan∠APD的值为______.
科目:初中数学 来源: 题型:
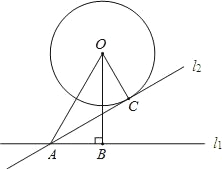
【题目】如图,⊙O与直线l1相离,圆心O到直线l1的距离OB=2![]() ,OA=4,将直线l1绕点A逆时针旋转30°后得到的直线l2刚好与⊙O相切于点C,则OC=_____.
,OA=4,将直线l1绕点A逆时针旋转30°后得到的直线l2刚好与⊙O相切于点C,则OC=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
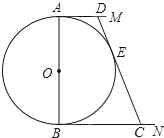
【题目】如图,⊙O的直径AB=12cm,AM和BN是它的两条切线,DE切⊙O于E,交AM于D,BN于C,设AD=x,BC=y,求y与x的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
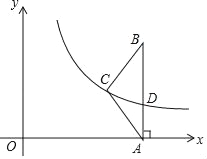
【题目】如图,在△ABC中,AC=BC=5,AB=8,AB⊥x轴,垂足为A,反比例函数y=![]() (x>0)的图象经过点C,交AB于点D.
(x>0)的图象经过点C,交AB于点D.
(1)若OA=AB,求k的值;
(2)若BC=BD,连接OC,求△OAC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 如图,△ABC为等腰直角三角形,∠BAC=90°,BC=1,E为直角边AB上任意一点,以线段CE为斜边作等腰Rt△CDE,连接AD,下列说法:①AC⊥ED;②∠BCE=∠ACD;③△AED∽△ECB;④AD∥BC;⑤四边形ABCD面积的最大值为![]() ,其中正确的是______________.
,其中正确的是______________.
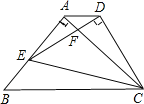
查看答案和解析>>
科目:初中数学 来源: 题型:
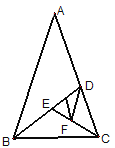
【题目】如图,顶角为36°的等腰三角形,其底边与腰之比等![]() ,这样的三角形称为黄金三角形,已知腰AB=1,△ABC为第一个黄金三角形,△BCD为第二个黄金三角形,△CDE为第三个黄金三角形,以此类推,第2014个黄金三角形的周长( )
,这样的三角形称为黄金三角形,已知腰AB=1,△ABC为第一个黄金三角形,△BCD为第二个黄金三角形,△CDE为第三个黄金三角形,以此类推,第2014个黄金三角形的周长( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,线段AB=1,点P1是线段AB的黄金分割点(且AP1<BP1,即P1B2=AP1AB),点P2是线段AP1的黄金分割点(AP2<P1P2),点P3是线段AP2的黄金分割点(AP3<P2P3),…,依此类推,则线段AP2017的长度是( )
![]()
A. (![]() )2017 B. (
)2017 B. (![]() )2017 C. (
)2017 C. (![]() )2017 D. (
)2017 D. (![]() ﹣2)1008
﹣2)1008
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b的图象与反比例函数![]() (x>0)的图象交于A(2,﹣1),B(
(x>0)的图象交于A(2,﹣1),B(![]() ,n)两点,直线y=2与y轴交于点C.
,n)两点,直线y=2与y轴交于点C.

(1)求一次函数与反比例函数的解析式;
(2)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠B=90°,AB=12,BC=24,动点P从点A开始沿边AB向终点B以每秒2个单位长度的速度移动,动点Q从点B开始沿边BC以每秒4个单位长度的速度向终点C移动,如果点P、Q分别从点A、B同时出发,那么△PBQ的面积S随出发时间t(s)如何变化?写出函数关系式及t的取值范围.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com