
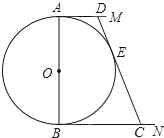
【题目】如图,⊙O的直径AB=12cm,AM和BN是它的两条切线,DE切⊙O于E,交AM于D,BN于C,设AD=x,BC=y,求y与x的函数关系式.
科目:初中数学 来源: 题型:
【题目】如图,在同一平面内,将两个全等的等腰直角![]() 和
和![]() 摆放在一起,
摆放在一起,![]() 为公共顶点,
为公共顶点,![]() ,它们的斜边长为2,若
,它们的斜边长为2,若![]() 固定不动,
固定不动,![]() 绕点
绕点![]() 旋转,
旋转,![]() 、
、![]() 与边
与边![]() 的交点分别为
的交点分别为![]() 、
、![]() (点
(点![]() 不与点
不与点![]() 重合,点
重合,点![]() 不与点
不与点![]() 重合),设
重合),设![]() ,
,![]() .
.

(1)请在图中找出两对相似而不全等的三角形,并选取其中一对加以证明.
(2)求![]() 与
与![]() 的函数关系式,直接写出自变量
的函数关系式,直接写出自变量![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A、B、C、D均在⊙O上,FB与⊙O相切于点B,AB与CF交于点G,OA⊥CF于点E,AC∥BF.
(1)求证:FG=FB.
(2)若tan∠F=![]() ,⊙O的半径为4,求CD的长.
,⊙O的半径为4,求CD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着新农村的建设和旧城的改造,我们的家园越来越美丽,小明家附近广场中央新修了一个圆形喷水池,在水池中心竖直安装了一根高![]() 米的喷水管,它喷出的抛物线形水柱在与池中心的水平距离为米处达到最高,水柱落地处离池中心
米的喷水管,它喷出的抛物线形水柱在与池中心的水平距离为米处达到最高,水柱落地处离池中心![]() 米.
米.

(1)请你建立适当的直角坐标系,并求出水柱抛物线的函数解析式;
(2)求出水柱的最大高度是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
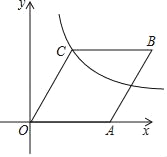
【题目】如图,在平面直角坐标系中,四边形OABC是菱形,∠B=60°,反比例函数y=![]() (k>0)的图象经过点C,若将菱形向下平移2个单位,点B恰好落在反比例函数的图象上,则反比例函数的表达式为( )
(k>0)的图象经过点C,若将菱形向下平移2个单位,点B恰好落在反比例函数的图象上,则反比例函数的表达式为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
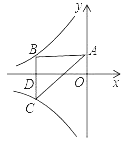
【题目】如图所示双曲线y=![]() 与y=﹣
与y=﹣![]() 分别位于第三象限和第二象限,A是y轴上任意一点,B是y=﹣
分别位于第三象限和第二象限,A是y轴上任意一点,B是y=﹣![]() 上的点,C是y=
上的点,C是y=![]() 上的点,线段BC⊥x轴于D,且4BD=3CD,则下列说法:①双曲线y=
上的点,线段BC⊥x轴于D,且4BD=3CD,则下列说法:①双曲线y=![]() 在每个象限内,y随x的增大而减小;②若点B的横坐标为﹣3,则C点的坐标为(﹣3,
在每个象限内,y随x的增大而减小;②若点B的横坐标为﹣3,则C点的坐标为(﹣3,![]() );③k=4;④△ABC的面积为定值7,正确的有( )
);③k=4;④△ABC的面积为定值7,正确的有( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
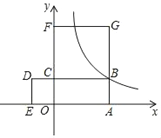
【题目】如图,点B是反比例函数图象上的一点,矩形OABC的周长是16,正方形BCFG和正方形OCDE的面积之和为32,则反比例函数的解析式为( )
A. y=![]() B. y=
B. y=![]() C. y=
C. y=![]() D. y=
D. y=![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
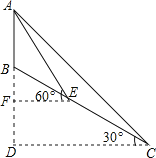
【题目】如图,小山顶上有一信号塔AB,山坡BC的倾角为30°,现为了测量塔高AB,测量人员选择山脚C处为一测量点,测得塔顶仰角为45°,然后顺山坡向上行走100米到达E处,再测得塔顶仰角为60°,求塔高AB.(结果保留整数![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com