
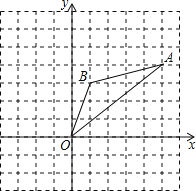
【题目】在如图的直角坐标系中,已知点A(2,0)、B(0,-4),将线段AB绕点A按逆时针方向旋转90°至AC.

(1)求点C的坐标;
(2)若抛物线y=-x2+ax+4经过点C.
①求抛物线的解析式;
②在抛物线上是否存在点P(点C除外)使△ABP是以AB为直角边的等腰直角三角形?若存在,求出所有点P的坐标;若不存在,请说明理由.
【答案】C的坐标为(3,﹣1);
(2)①抛物线的解析式为y=﹣![]() x2+
x2+![]() x+2;
x+2;
②存在点P,△ABP是以AB为直角边的等腰直角三角形,符合条件的点有P1(﹣1,1),P2(﹣2,﹣1)两点.
【解析】
试题(1)过点C作CD垂直于x轴,由线段AB绕点A按逆时针方向旋转90°至AC,根据旋转的旋转得到AB=AC,且∠BAC为直角,可得∠OAB与∠CAD互余,由∠AOB为直角,可得∠OAB与∠ABO互余,根据同角的余角相等可得一对角相等,再加上一对直角相等,利用ASA可证明三角形ACD与三角形AOB全等,根据全等三角形的对应边相等可得AD=OB,CD=OA,由A和B的坐标及位置特点求出OA及OB的长,可得出OD及CD的长,根据C在第四象限得出C的坐标;
(2)①由已知的抛物线经过点C,把第一问求出C的坐标代入抛物线解析式,列出关于a的方程,求出方程的解得到a的值,确定出抛物线的解析式;
②假设存在点P使△ABP是以AB为直角边的等腰直角三角形,分三种情况考虑:(i)A为直角顶点,过A作AP1垂直于AB,且AP1=AB,过P1作P1M垂直于x轴,如图所示,根据一对对顶角相等,一对直角相等,AB=AP1,利用AAS可证明三角形AP1M与三角形ACD全等,得出AP1与P1M的长,再由P1为第二象限的点,得出此时P1的坐标,代入抛物线解析式中检验满足;(ii)当B为直角顶点,过B作BP2垂直于BA,且BP2=BA,过P2作P2N垂直于y轴,如图所示,同理证明三角形BP2N与三角形AOB全等,得出P2N与BN的长,由P2为第三象限的点,写出P2的坐标,代入抛物线解析式中检验满足;(iii)当B为直角顶点,过B作BP3垂直于BA,且BP3=BA,如图所示,过P3作P3H垂直于y轴,同理可证明三角形P3BH全等于三角形AOB,可得出P3H与BH的长,由P3为第四象限的点,写出P3的坐标,代入抛物线解析式检验,不满足,综上,得到所有满足题意的P的坐标.
试题解析:(1)过C作CD⊥x轴,垂足为D,
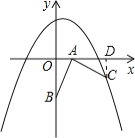
∵BA⊥AC,∴∠OAB+∠CAD=90°,
又∠AOB=90°,∴∠OAB+∠OBA=90°,
∴∠CAD=∠OBA,又AB=AC,∠AOB=∠ADC=90°,
∴△AOB≌△CDA,又A(1,0),B(0,﹣2),
∴OA=CD=1,OB=AD=2,
∴OD=OA+AD=3,又C为第四象限的点,
∴C的坐标为(3,﹣1);
(2)①∵抛物线y=﹣![]() x2+ax+2经过点C,且C(3,﹣1),
x2+ax+2经过点C,且C(3,﹣1),
∴把C的坐标代入得:﹣1=﹣![]() +3a+2,解得:a=
+3a+2,解得:a=![]() ,
,
则抛物线的解析式为y=﹣![]() x2+
x2+![]() x+2;
x+2;
②存在点P,△ABP是以AB为直角边的等腰直角三角形,
(i)若以AB为直角边,点A为直角顶点,
则延长CA至点P1使得P1A=CA,得到等腰直角三角形ABP1,过点P1作P1M⊥x轴,如图所示,
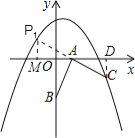
∵AP1=CA,∠MAP1=∠CAD,∠P1MA=∠CDA=90°,
∴△AMP1≌△ADC,
∴AM=AD=2,P1M=CD=1,
∴P1(﹣1,1),经检验点P1在抛物线y=﹣![]() x2+
x2+![]() x+2上;
x+2上;
(ii)若以AB为直角边,点B为直角顶点,则过点B作BP2⊥BA,且使得BP2=AB,
得到等腰直角三角形ABP2,过点P2作P2N⊥y轴,如图,
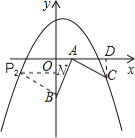
同理可证△BP2N≌△ABO,
∴NP2=OB=2,BN=OA=1,
∴P2(﹣2,﹣1),经检验P2(﹣2,﹣1)也在抛物线y=﹣![]() x2+
x2+![]() x+2上;
x+2上;
(iii)若以AB为直角边,点B为直角顶点,则过点B作BP3⊥BA,且使得BP3=AB,
得到等腰直角三角形ABP3,过点P3作P3H⊥y轴,如图,
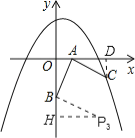
同理可证△BP3H≌△BAO,
∴HP3=OB=2,BH=OA=1,
∴P3(2,﹣3),经检验P3(2,﹣3)不在抛物线y=﹣![]() x2+
x2+![]() x+2上;
x+2上;
则符合条件的点有P1(﹣1,1),P2(﹣2,﹣1)两点.


科目:初中数学 来源: 题型:
【题目】某校实施课程改革,为初三学生设置了A,B,C,D,E,F共六门不同的拓展性课程,现随机抽取若干学生进行了“我最想选的一门课”调查,并将调查结果绘制成如图统计图表(不完整)
选修课 | A | B | C | D | E | F |
人数 | 20 | 30 |
根据图标提供的信息,下列结论错误的是( )

A. 这次被调查的学生人数为200人 B. 扇形统计图中E部分扇形的圆心角为72°
C. 被调查的学生中最想选F的人数为35人 D. 被调查的学生中最想选D的有55人
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点P(﹣2,3)是反比例函数y=![]() 图象上的一点,则下列各点中,也在该函数图象上的是( )
图象上的一点,则下列各点中,也在该函数图象上的是( )
A. (2,﹣3) B. (3,2) C. (﹣2,﹣3) D. (2,3)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小赵投资销售一种进价为每件20元的护眼台灯.销售过程中发现,当月内销售单价不变,则月销售量y(件)与销售单价x(元)之间的关系可近似的看作一次函数:![]() .
.
(1)设小赵每月获得利润为w(元),当销售单价定为多少元时,每月可获得最大利润?并求出最大利润.
(2)如果小赵想要每月获得的利润不低于2000元,那么如何制定销售单价才可以实现这一目标?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】双十一购物节即将到来,某商场设计了两种的促销方案,并有以下两种销售量预期.预期一:第1步,销售量扩大为原来的a倍.第2步,再扩大为第1步销售量的b倍.预期二:第1步,销售量扩大为原来的![]() 倍;第2步,再扩大为第1步销售量的
倍;第2步,再扩大为第1步销售量的![]() 倍;其中a,b为不相等的正数,请问两种预期中,哪种销售量更多?试说明理由.
倍;其中a,b为不相等的正数,请问两种预期中,哪种销售量更多?试说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为1的正方形组成的网格中,△AOB的顶点均在格点上,其中点A(5,4),B(1,3),将△AOB绕点O逆时针旋转90°后得到△A1OB1.
(1)画出△A1OB1;
(2)在旋转过程中点B所经过的路径长为______;
(3)求在旋转过程中线段AB、BO扫过的图形的面积之和.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】太原是一座具有4700多年历史、2500年建城史的历史古都,系有“锦绣太原城”的美誉,在“我可爱的家乡”主题班会中,主持人准备了“晋祠园林”、“崇山大佛”、“龙山石窟”、“凌霄双塔”这四处景点的照片各一张,并将它们背面朝上放置(照片背面完全相同),甲同学从中随机抽取一张,不放回,乙再从剩下的照片中随机抽取一张,若要根据抽取的照片作相关景点介绍,求甲、乙两人中恰好有一人介绍“晋祠园林”的概率.(提示:可用照片序号列表或画树状图)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com