
【题目】小赵投资销售一种进价为每件20元的护眼台灯.销售过程中发现,当月内销售单价不变,则月销售量y(件)与销售单价x(元)之间的关系可近似的看作一次函数:![]() .
.
(1)设小赵每月获得利润为w(元),当销售单价定为多少元时,每月可获得最大利润?并求出最大利润.
(2)如果小赵想要每月获得的利润不低于2000元,那么如何制定销售单价才可以实现这一目标?
【答案】(1)当销售单价定为35元时,每月获得的利润最大,最大利润为2250元;
(2)如果小赵想要每月获得的利润不低于2000元,那么他的销售单价应不低于30元而不高于40元.
【解析】
试题(1)根据总利润=单利润×销售量即可得到函数关系式,再根据二次函数的性质即得结果;
(2)先求得利润为2000元时对应的销售单价,再根据二次函数的性质即可求得结果.
(1)由题意得w=(x-20)·y=(x-20)·(![]() )
)![]()
当![]() 时,
时,![]() ;
;
(2)由题意得![]()
解得x1 =30,x2 =40
即小赵想要每月获得2000元的利润,销售单价应定为30元或40元
∵![]()
∴抛物线开口向下
∴当30≤x≤40时,w≥2000
答:(1)当销售单价定为35元时,每月可获得最大利润,且最大利润为2250元;
(2)如果小赵想要每月获得的利润不低于2000元,那么他的销售单价应不低于30元而不高于40元.


 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案科目:初中数学 来源: 题型:
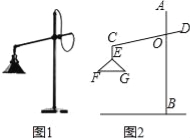
【题目】如图1所示的是一种置于桌面上的简易台灯,将其结构简化成图2,灯杆AB与CD交于点O(点O固定),灯罩连杆CE始终保持与AB平行,灯罩下方FG处于水平位置,测得OC=20cm,∠COB=70°,∠F=40°,EF=EG,点G到OB的距离为12cm.
(1)求∠CEG的度数.
(2)求灯罩的宽度(FG的长;结果精确到0.1cm,可用科学计算器).
(参考数据:sin40°≈0.643,cos40°≈0.766,sin70°≈0.940,cos70°≈0.342)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场试销一种成本为8元/千克的水果,经试销发现,销量y(千克)与销售单价x(元)符合一次函数y=kx+b,且当x=10时,y=300;当x=13时,y=150.
(1)求y(千克)与x(元)(x>8)的函数关系式;
(2)设该超市销售这种水果每天获取的利润为W元,那么当销售单价为何值时,每天可获得的利润最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在如图的直角坐标系中,已知点A(2,0)、B(0,-4),将线段AB绕点A按逆时针方向旋转90°至AC.

(1)求点C的坐标;
(2)若抛物线y=-x2+ax+4经过点C.
①求抛物线的解析式;
②在抛物线上是否存在点P(点C除外)使△ABP是以AB为直角边的等腰直角三角形?若存在,求出所有点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
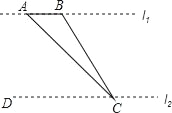
【题目】如图,某数学兴趣小组为了测量河对岸l1的两棵古树A、B之间的距离,他们在河这边沿着与AB平行的直线l2上取C、D两点,测得∠ACB=15°,∠ACD=45°,若l1、l2之间的距离为50m,则古树A、B之间的距离为_____m.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在平面直角坐标系内,△ABC各顶点的坐标分别是A(﹣2,4),B(﹣4,3),C(﹣1,1).将△ABC向右平移5个单位长度,再向下平移4个单位长度得到△A′B′C′.
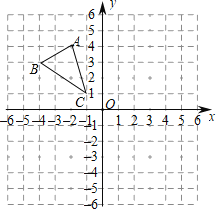
(1)请作出平移后的△A′B′C′,并写出△A′B′C′各顶点的坐标;
(2)如果将△A′B′C′看成是由△ABC经过一次平移得到的,请指出这一平移的平移方向和平移距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为宣传“扫黑除恶”专项行动,社区准备制作一幅宣传版面,喷绘时为了美观,要在矩形图案四周外围增加一圈等宽的白边,已知图案的长为2米,宽为1米,图案面积占整幅宣传版面面积的90%,若设白边的宽为x米,则根据题意可列出方程( )

A. 90%×(2+x)(1+x)=2×1 B. 90%×(2+2x)(1+2x)=2×1
C. 90%×(2﹣2x)(1﹣2x)=2×1 D. (2+2x)(1+2x)=2×1×90%
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com