练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

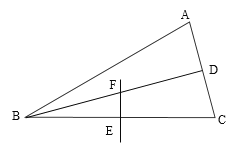
    【题目】如图，在中，平分交于点的垂直平分线交于点，交于点，若，则的长为__________．

    【答案】6

    【解析】

    连接CF，根据等腰三角形的性质，得到∠ABD=∠CBD=15°，BD⊥AC，AD=CD，再由垂直平分线的性质得到BF=CF=6，再根据三角形的外角的性质得到∠CFD=∠CBD+∠BCF=30°，由30°的直角三角形的性质得出CD，即可求出AC的长度．

    解：连接CF，∵，BD是∠ABC的平分线，，

    ∴∠ABD=∠CBD=15°，BD⊥AC，AD=CD

    ∵EF垂直平分BC，

    ∴BF=CF=6

    ∴∠CBD=∠BCF=15°，

    ∴∠CFD=∠CBD+∠BCF=30°，

    ∴在Rt△CFD中，CD=，

    ∴AC=2CD=6，

    故答案为：6．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

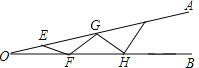
    【题目】如图，∠AOB是一钢架，∠AOB＝15°，为使钢架更加牢固，需在其内部添加一些钢管EF、FG、GH，添的钢管长度都与OE相等，则最多能添加这样的钢管_____根．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，湛河两岸AB与EF平行，小亮同学假期在湛河边A点处，测得对岸河边C处视线与湛河岸的夹角∠CAB=37°，沿河岸前行140米到点B处，测得对岸C处的视线与湛河岸夹角∠CBA=45°.问湛河的宽度约多少米?(参考数据：sin37°≈0.60，cos37°=0.80，tan37°=0.75)

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】今年5月，某大型商业集团随机抽取所属的部分商业连锁店进行评估，将抽取的各商业连锁店按照评估成绩分成了、、、四个等级，并绘制了如下不完整的扇形统计图和条形统计图.

    根据以上信息，解答下列问题：

    （1）本次评估随机抽取了多少家商业连锁店？

    （2）请补充完整扇形统计图和条形统计图，并在图中标注相应数据；

    （3）从、两个等级的商业连锁店中任选2家介绍营销经验，求其中至少有一家是等级的概率.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

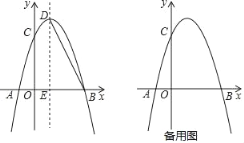
    【题目】如图，抛物线y=﹣x2+bx+c与x轴交于点A和点B，与y轴交于点C，点B坐标为（6，0），点C坐标为（0，6），点D是抛物线的顶点，过点D作x轴的垂线，垂足为E，连接BD．

    （1）求抛物线的解析式及点D的坐标；

    （2）点F是抛物线上的动点，当∠FBA=∠BDE时，求点F的坐标；

    （3）若点P是x轴上方抛物线上的动点，以PB为边作正方形PBFG，随着点P的运动，正方形的大小、位置也随着改变，当顶点F或G恰好落在y轴上时，请直接写出点P的横坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】小赵投资销售一种进价为每件20元的护眼台灯．销售过程中发现,当月内销售单价不变,则月销售量y（件）与销售单价x（元）之间的关系可近似的看作一次函数：．

    (1)设小赵每月获得利润为w（元）,当销售单价定为多少元时,每月可获得最大利润？并求出最大利润.

    (2)如果小赵想要每月获得的利润不低于2000元,那么如何制定销售单价才可以实现这一目标？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】对于多项式Ax2bxc（b、c为常数），作如下探究：

    （1）不论x取何值，A都是非负数，求b与c满足的条件；

    （2）若A是完全平方式，

    ①当c=9时，b= ;当b=3时，c= ;

    ②若多项式Bx2dxc与A有公因式，求d的值.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某县为了落实中央的“强基惠民工程”，计划将某村的居民自来水管道进行改造．该工程若由甲队单独施工恰好在规定时间内完成；若乙队单独施工，则完成工程所需天数是规定天数的1．5倍．如果由甲、乙队先合做15天，那么余下的工程由甲队单独完成还需5天．

    （1）这项工程的规定时间是多少天？

    （2）已知甲队每天的施工费用为6500元，乙队每天的施工费用为3500元．为了缩短工期以减少对居民用水的影响，工程指挥部最终决定该工程由甲、乙队合做来完成．则该工程施工费用是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC和△DEF中，已有条件AB=DE，还需要添加两个条件才能使△ABC≌△DEF．不能添加的一组条件是（ ）

    A. ∠B=∠E，BC=EF B. ∠A=∠D，BC=EF

    C. ∠A=∠D，∠B=∠E D. BC=EF，AC=DF

    查看答案和解析>>

    同步练习册答案