
【题目】对于多项式Ax2bxc(b、c为常数),作如下探究:
(1)不论x取何值,A都是非负数,求b与c满足的条件;
(2)若A是完全平方式,
①当c=9时,b= ;当b=3时,c= ;
②若多项式Bx2dxc与A有公因式,求d的值.
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A(-2,4),B(4,2),在x轴上取一点P,使点P到点A和点B的距离之和最小,则点P的坐标是( )

A. (-2,0) B. (0,0) C. (2,0) D. (4,0)
查看答案和解析>>
科目:初中数学 来源: 题型:
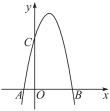
【题目】如图,一个二次函数的图象经过A,B,C三点,点A的坐标为(-1,0),点B的坐标为(4,0),点C在y轴的正半轴上,且AB=OC.
(1)求点C的坐标;
(2)求这个二次函数的解析式,并求出该函数的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O中,直径CD⊥弦AB于E,AM⊥BC于M,交CD于N,连接AD.
(1)求证:AD=AN;
(2)若AB=8,ON=1,求⊙O的半径.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题中错误的是( )
A. 圆柱的轴截面是过母线的截面中面积最大的一个
B. 圆锥的轴截面是所有过顶点的截面中面积最大的一个
C. 圆台的所有平行于底面的截面都是圆
D. 圆锥所有的轴截面是全等的等腰三角形
查看答案和解析>>
科目:初中数学 来源: 题型:
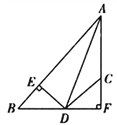
【题目】如图,AD平分∠BAC,DE⊥AB于点E,DF⊥AC于点F,且BD=CD.
(1)图中与△BDE全等的三角形是 ,请加以证明;
(2)若AE=6 cm,AC=4 cm,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
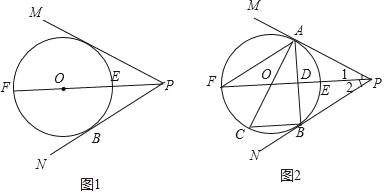
【题目】如图1,已知∠MPN的角平分线PF经过圆心O交⊙O于点E、F,PN是⊙O的切线,B为切点.
(1)求证:PM也是⊙O的切线;
(2)如图2,在(1)的前提下,设切线PM与⊙O的切点为A,连接AB交PF于点D;连接AO交⊙O于点C,连接BC,AF;记∠PFA为∠α.
①若BC=6,tan∠α=![]() ,求线段AD的长;
,求线段AD的长;
②小华探究图2之后发现:EF2=mODOP(m为正整数),请你猜想m的数值?并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料1:
对于两个正实数![]() ,由于
,由于![]() ,所以
,所以![]() ,即
,即![]() ,所以得到
,所以得到![]() ,并且当
,并且当![]() 时,
时,![]()
阅读材料2:
若![]() ,则
,则![]() ,因为
,因为![]() ,
,![]() ,所以由阅读材料1可得:
,所以由阅读材料1可得:![]() ,即
,即![]() 的最小值是2,只有
的最小值是2,只有![]() 时,即
时,即![]() =1时取得最小值.
=1时取得最小值.
根据以上阅读材料,请回答以下问题:
(1)比较大小
![]()
![]() (其中
(其中![]() ≥1);
≥1); ![]() -2(其中
-2(其中![]() <-1)
<-1)
(2)已知代数式![]() 变形为
变形为![]() ,求常数
,求常数![]() 的值
的值
(3)当![]() = 时,
= 时,![]() 有最小值,最小值为 (直接写出答案).
有最小值,最小值为 (直接写出答案).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,射线OM在第一象限,且与x轴正半轴的夹角为60°,过点D(6,0)作DA⊥OM于点A,作线段 OD的垂直平分线BE交x轴于点E,交AD于点B,作射线OB.以AB为边在△AOB的外侧作正方形ABCA1,延长A1C交射线OB于点B1,以A1B1为边在△A1OB1的外侧作正方形A1B1C1A2,延长A2C1交射线OB于点B2,以A2B2为边在△A2OB2的外侧作正方形A2B2C2A3……按此规律进行下去,则正方形A2017B2017C2017A2018的周长为______________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com