
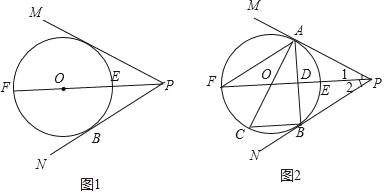
ЁОЬтФПЁПШчЭМ1ЃЌвбжЊЁЯMPNЕФНЧЦНЗжЯпPFОЙ§дВаФOНЛЁбOгкЕуEЁЂFЃЌPNЪЧЁбOЕФЧаЯпЃЌBЮЊЧаЕуЃЎ
ЃЈ1ЃЉЧѓжЄЃКPMвВЪЧЁбOЕФЧаЯпЃЛ
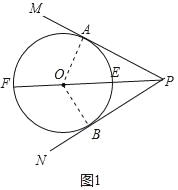
ЃЈ2ЃЉШчЭМ2ЃЌдкЃЈ1ЃЉЕФЧАЬсЯТЃЌЩшЧаЯпPMгыЁбOЕФЧаЕуЮЊAЃЌСЌНгABНЛPFгкЕуDЃЛСЌНгAOНЛЁбOгкЕуCЃЌСЌНгBCЃЌAFЃЛМЧЁЯPFAЮЊЁЯІСЃЎ
ЂйШєBC=6ЃЌtanЁЯІС=![]() ЃЌЧѓЯпЖЮADЕФГЄЃЛ
ЃЌЧѓЯпЖЮADЕФГЄЃЛ
ЂкаЁЛЊЬНОПЭМ2жЎКѓЗЂЯжЃКEF2=mODOPЃЈmЮЊе§ећЪ§ЃЉЃЌЧыФуВТЯыmЕФЪ§жЕЃПВЂжЄУїФуЕФНсТлЃЎ
ЁОД№АИЁПЃЈ1ЃЉЯъМћНтЮіЃЛЃЈ2ЃЉЂй4ЃЛЂк4.
ЁОНтЮіЁП
ЃЈ1ЃЉЙ§ЕуOзїOAЁЭPMЃЌДЙзуЮЊAЃЌСЌНгOBЃЌИљОнЧаЯпЕФаджЪПЩЕУГіOBЪЧЁбOЕФАыОЖЧвOBЁЭPNЃЌгЩPFЦНЗжЁЯMPNРћгУНЧЦНЗжЯпЕФаджЪПЩЕУГіOA=OBЃЌНјЖјПЩжЄГіPMвВЪЧЁбOЕФЧаЯпЃЛ
ЃЈ2ЃЉЂйгЩPMЁЂPNЖМЪЧЁбOЕФЧаЯпПЩЕУГіPA=PBЃЌРћгУЕШбќШ§НЧаЮЕФШ§ЯпКЯвЛПЩЕУГіOPЁЭABЁЂAD=BDЃЌгЩШ§НЧаЮжаЮЛЯпЕФаджЪПЩЕУГіOD=3ЃЌЩшЁбOЕФАыОЖЮЊrЃЌдђFD=r+3ЃЌAD=![]() ЃЈr+3ЃЉЃЌдкRtЁїAODжаЃЌРћгУЙДЙЩЖЈРэПЩЧѓГіrЕФжЕЃЌНЋЦфДњШыAD=
ЃЈr+3ЃЉЃЌдкRtЁїAODжаЃЌРћгУЙДЙЩЖЈРэПЩЧѓГіrЕФжЕЃЌНЋЦфДњШыAD=![]() ЃЈr+3ЃЉжаМДПЩЧѓГіADЕФГЄЖШЃЛ
ЃЈr+3ЃЉжаМДПЩЧѓГіADЕФГЄЖШЃЛ
ЂкгЩЁЯOAP=ЁЯODA=90ЁуЁЂЁЯAOP=ЁЯDOAПЩжЄГіЁїOAPЁзЁїODAЃЌРћгУЯрЫЦШ§НЧаЮЕФаджЪПЩЕУГіOA2=ODOPЃЌНсКЯEF=2OAПЩжЄГіEF2=4ODOPЃЌМДm=4ЃЎ
ЃЈ1ЃЉжЄУїЃКдкЭМ1жаЃЌЙ§ЕуOзїOAЁЭPMЃЌДЙзуЮЊAЃЌСЌНгOBЃЎ
ЁпPNЪЧЁбOЕФЧаЯпЃЌBЮЊЧаЕуЃЌ
ЁрOBЪЧЁбOЕФАыОЖЃЌЧвOBЁЭPNЃЎ
ЁпPFЦНЗжЁЯMPNЃЌ
ЁрOA=OBЃЌ
ЁрPMвВЪЧЁбOЕФЧаЯпЃЛ
ЃЈ2ЃЉЂйЁпPMЁЂPNЖМЪЧЁбOЕФЧаЯпЃЌ
ЁрPA=PBЃЎ
ЁпЁЯAPD=ЁЯBPDЃЌ
ЁрOPЁЭABЃЌAD=BDЃЎ
ЁпODЮЊЁїABCЕФжаЮЛЯпЃЌ
ЁрOD=![]() BC=3ЃЎ
BC=3ЃЎ
ЩшЁбOЕФАыОЖЮЊrЃЌдђFD=r+3ЃЌ
ЁпtanЁЯІС=![]() ЃЌ
ЃЌ
ЁрAD=![]() ЃЈr+3ЃЉЃЎ
ЃЈr+3ЃЉЃЎ
дкRtЁїAODжаЃЌOA2=AD2+OD2ЃЌМДr2=[![]() ЃЈr+3ЃЉ]2+32ЃЌ
ЃЈr+3ЃЉ]2+32ЃЌ
НтЕУЃКr=5ЃЌ
ЁрAD=![]() ЃЈr+3ЃЉ=4ЃЎ
ЃЈr+3ЃЉ=4ЃЎ
ЂкВТЯыm=4ЃЎ
жЄУїЃКЁпЁЯOAP=ЁЯODA=90ЁуЃЌЁЯAOP=ЁЯDOAЃЌ
ЁрЁїOAPЁзЁїODAЃЌ
Ёр![]() ЃЌМДOA2=ODOPЃЌ
ЃЌМДOA2=ODOPЃЌ
гжЁпEF=2OAЃЌ
ЁрEF2=4ODOPЃЌ
Ёрm=4ЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЃКШчЭМЃЌвЛПщRtЁїABCЕФТЬЕиЃЌСПЕУСНжБНЧБпAC=8cmЃЌBC=6cm.ЯждквЊНЋетПщТЬЕиРЉГфГЩЕШбќЁїABDЃЌЧвРЉГфВПЗжЃЈЁїADCЃЉЪЧвд8cmЮЊжБНЧБпГЄЕФжБНЧШ§НЧаЮЃЌЧѓРЉГфЕШбќЁїABDЕФжмГЄ.
ЃЈ1ЃЉдкЭМ1жаЃЌЕБAB=AD=10cmЪБЃЌЁїABDЕФжмГЄЮЊ ЃЎ
ЃЈ2ЃЉдкЭМ2жаЃЌЕБBA=BD=10cmЪБЃЌЁїABDЕФжмГЄЮЊ ЃЎ
ЃЈ3ЃЉдкЭМ3жаЃЌЕБDA=DBЪБЃЌЧѓЁїABDЕФжмГЄ.

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЕШБпЁїABCжаADЁЭBCЃЌAD=12,ШєЕуPдкЯпЖЮADЩЯдЫЖЏЃЌЕБ![]() AP+BPЕФжЕзюаЁЪБЃЌAPЕФГЄЮЊЃЈ ЃЉ.
AP+BPЕФжЕзюаЁЪБЃЌAPЕФГЄЮЊЃЈ ЃЉ.

A.4B.8C.10D.12
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЖдгкЖрЯюЪНAx2bxcЃЈbЁЂcЮЊГЃЪ§ЃЉЃЌзїШчЯТЬНОПЃК
ЃЈ1ЃЉВЛТлxШЁКЮжЕЃЌAЖМЪЧЗЧИКЪ§ЃЌЧѓbгыcТњзуЕФЬѕМўЃЛ
ЃЈ2ЃЉШєAЪЧЭъШЋЦНЗНЪНЃЌ
ЂйЕБc=9ЪБЃЌb= ;ЕБb=3ЪБЃЌc= ;
ЂкШєЖрЯюЪНBx2dxcгыAгаЙЋвђЪНЃЌЧѓdЕФжЕ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЯТБэЪЧ2018ФъШ§дТЗнФГОгУёаЁЧјЫцЛњГщШЁ20ЛЇОгУёЕФгУЫЎЧщПіЃК
дТгУЫЎСП/Жж | 15 | 20 | 25 | 30 | 35 | 40 | 45 |
ЛЇЪ§ | 2 | 4 | m | 4 | 3 | 0 | 1 |
ЃЈ1ЃЉЧѓГіm=ЁЁ ЁЁЃЌВЙГфЛГіет20ЛЇМвЭЅШ§дТЗнгУЕчСПЕФЬѕаЮЭГМЦЭМЃЛ
ЃЈ2ЃЉОнЩЯБэжагаЙиаХЯЂЃЌМЦЫуЛђевГіЯТБэжаЕФЭГМЦСПЃЌВЂНЋНсЙћЬюШыБэжаЃК
ЭГМЦСПУћГЦ | жкЪ§ | жаЮЛЪ§ | ЦНОљЪ§ |
Ъ§Он | ЁЁ ЁЁ | ЁЁ ЁЁ | ЁЁ ЁЁ |
ЃЈ3ЃЉЮЊСЫГЋЕМЁАНкдМгУЫЎЃЌТЬЩЋЛЗБЃЁБЕФвтЪЖЃЌНИгЪаздРДЫЎЙЋЫОЪЕааЁАЬнМЖгУЫЎЁЂЗжРрМЦЗбЁБЃЌМлИёБэШчЯТЃК
дТгУЫЎЬнМЖБъзМ | ЂёМЖЃЈ30ЖжвдФкЃЉ | ЂђМЖЃЈГЌЙ§30ЖжЕФВПЗжЃЉ |
ЕЅМлЃЈдЊ/ЖжЃЉ | 2.4 | 4 |
ШчЙћИУаЁЧјга500ЛЇМвЭЅЃЌИљОнвдЩЯЪ§ОнЃЌЧыЙРЫуИУаЁЧјШ§дТЗнгаЖрЩйЛЇМвЭЅДяЕНЂђМЖБъзМЃПВЂЙРЫуетаЉЂђМЖгУЫЎЛЇЕФзмЫЎЗбЪЧЖрЩйдЊЃП

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдФЖСВФСЯЃЌЛиД№ЮЪЬтЃЎ
ВФСЯЃКЮЊНтЗНГЬx4Ѓx2Ѓ6ЃН0ЃЌПЩНЋЗНГЬБфаЮЮЊ(x2)2Ѓx2Ѓ6ЃН0ЃЌШЛКѓЩшx2ЃНyЃЌдђ(x2)2ЃНy2ЃЌдЗНГЬЛЏЮЊy2ЃyЃ6ЃН0ЂйЃЌ
НтЕУy1ЃНЃ2ЃЌy2ЃН3.
ЕБy1ЃНЃ2ЪБЃЌx2ЃНЃ2ЮовтвхЃЌЩсШЅЃЛЕБy2ЃН3ЪБЃЌx2ЃН3ЃЌНтЕУxЃНЁР![]() .
.
ЫљвдЃЌдЗНГЬЕФНтЮЊx1ЃН![]() ЃЌx2ЃНЃ
ЃЌx2ЃНЃ![]() .
.
ЮЪЬтЃК
(1)дкгЩдЗНГЬЕУЕНЗНГЬЂйЕФЙ§ГЬжаЃЌРћгУ ЗЈДяЕНСЫНЕДЮЕФФПЕФЃЌЬхЯжСЫ ЕФЪ§бЇЫМЯыЃЛ
(2)РћгУБОЬтЕФНтЬтЗНЗЈЃЌНтЗНГЬ(x2Ѓx)2Ѓ4(x2Ѓx)Ѓ12ЃН0.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮвУЧжЊЕРЃЌгаРэЪ§АќРЈећЪ§ЁЂгаЯоаЁЪ§КЭЮоЯобЛЗаЁЪ§ЃЌЪТЪЕЩЯЃЌЫљгаЕФгаРэЪ§ЖМПЩвдЛЏЮЊЗжЪ§аЮЪНЃЈећЪ§ПЩПДзїЗжФИЮЊ1ЕФЗжЪ§ЃЉЃЌФЧУДЮоЯобЛЗаЁЪ§ШчКЮБэЪОЮЊЗжЪ§аЮЪНФиЃПЧыПДвдЯТЪОР§ЃК
Р§ЃКНЋ![]() ЛЏЮЊЗжЪ§аЮЪН
ЛЏЮЊЗжЪ§аЮЪН
гЩгк![]() =0.777ЁЃЌЩшx=0.777ЁЂй
=0.777ЁЃЌЩшx=0.777ЁЂй
дђ10x=7.777ЁЂк
ЂкЉЂйЕУ9x=7ЃЌНтЕУx=![]() ЃЌгкЪЧЕУ
ЃЌгкЪЧЕУ![]() =
=![]() ЃЎ
ЃЎ
ЭЌРэПЩЕУ![]() =
=![]() ЃЌ
ЃЌ![]() =1+
=1+![]() =1+
=1+![]() ЃЌ
ЃЌ
ИљОнвдЩЯдФЖСЃЌЛиД№ЯТСаЮЪЬтЃКЃЈвдЯТМЦЫуНсЙћОљгУзюМђЗжЪ§БэЪОЃЉ
ЃЈЛљДЁбЕСЗЃЉ
ЃЈ1ЃЉ![]() =ЁЁ ЁЁЃЌ
=ЁЁ ЁЁЃЌ![]() =ЁЁ ЁЁЃЛ
=ЁЁ ЁЁЃЛ
ЃЈ2ЃЉНЋ![]() ЛЏЮЊЗжЪ§аЮЪНЃЌаДГіЭЦЕМЙ§ГЬЃЛ
ЛЏЮЊЗжЪ§аЮЪНЃЌаДГіЭЦЕМЙ§ГЬЃЛ
ЃЈФмСІЬсЩ§ЃЉ
ЃЈ3ЃЉ![]() =ЁЁ ЁЁЃЌ
=ЁЁ ЁЁЃЌ![]() =ЁЁ ЁЁЃЛ
=ЁЁ ЁЁЃЛ
ЃЈзЂЃК![]() =0.315315ЁЃЌ
=0.315315ЁЃЌ![]() =2.01818ЁЃЉ
=2.01818ЁЃЉ
ЃЈЬНЫїЗЂЯжЃЉ
ЃЈ4ЃЉЂйЪдБШНЯ![]() гы1ЕФДѓаЁЃК
гы1ЕФДѓаЁЃК![]() ЁЁ ЁЁ1ЃЈЬюЁАЃОЁБЁЂЁАЃМЁБЛђЁА=ЁБЃЉ
ЁЁ ЁЁ1ЃЈЬюЁАЃОЁБЁЂЁАЃМЁБЛђЁА=ЁБЃЉ
ЂкШєвбжЊ![]() =
=![]() ЃЌдђ
ЃЌдђ![]() =ЁЁ ЁЁЃЎ
=ЁЁ ЁЁЃЎ
ЃЈзЂЃК![]() =0.285714285714ЁЃЉ
=0.285714285714ЁЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдк![]() жаЃЌ
жаЃЌ![]() ЪЧ
ЪЧ![]() ЕФжаЕуЃЌ
ЕФжаЕуЃЌ![]() ЃЌ
ЃЌ![]() ЗжБ№ЪЧ
ЗжБ№ЪЧ![]() ЕФШ§ЕШЗжЕуЃЌ
ЕФШ§ЕШЗжЕуЃЌ![]() ЃЌ
ЃЌ![]() ЗжБ№НЛ
ЗжБ№НЛ![]() гк
гк![]() ЃЌ
ЃЌ![]() СНЕуЃЌдђ
СНЕуЃЌдђ![]() ЕШгкЃЈ ЃЉ
ЕШгкЃЈ ЃЉ
A. 3:2:1 B. 4:2:1 C. 5:2:1 D. 5:3:2
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЁїABCжаЃЌЁЯC=90Ёу,AEЦНЗжЁЯBACНЛBCгкЕуE,OЪЧABЩЯвЛЕуЃЌОЙ§A,EСНЕуЕФЁбOНЛABгкЕуDЃЌСЌНгDEЃЌзїЁЯDEAЕФЦНЗжЯпEFНЛЁбOгкЕуFЃЌСЌНгAF.
ЃЈ1ЃЉЧѓжЄЃКBCЪЧЁбOЕФЧаЯпЃЛ
ЃЈ2ЃЉШєsinЁЯEFA=![]() ,AF=
,AF=![]() ,ЧѓЯпЖЮACЕФГЄ.
,ЧѓЯпЖЮACЕФГЄ.

ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com