
【题目】已知等边△ABC中AD⊥BC,AD=12,若点P在线段AD上运动,当![]() AP+BP的值最小时,AP的长为( ).
AP+BP的值最小时,AP的长为( ).

A.4B.8C.10D.12
【答案】B
【解析】
过点P作PD⊥AC于D,过点B作BF⊥AC于F,根据等边三角形的性质可得:∠CAD=∠ABF=∠CBF=![]() ∠BAC=30°,从而可得:PD=
∠BAC=30°,从而可得:PD=![]() AP,故
AP,故![]() AP+BP的最小值即为PD+BP的最小值,根据垂线段最短的性质即可判断BF即为PD+BP的最小值,再根据30°所对的直角边是斜边的一半求AP即可.
AP+BP的最小值即为PD+BP的最小值,根据垂线段最短的性质即可判断BF即为PD+BP的最小值,再根据30°所对的直角边是斜边的一半求AP即可.
解:过点P作PD⊥AC于D,过点B作BF⊥AC于F,如下图所示
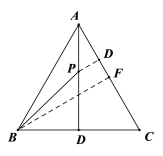
∵等边△ABC中AD⊥BC,
∴∠CAD=∠ABF=∠CBF=![]() ∠BAC=30°,
∠BAC=30°,
∴PD=![]() AP
AP
∴![]() AP+BP的最小值即为PD+BP的最小值
AP+BP的最小值即为PD+BP的最小值
∵在连接直线外一点与直线上各点的线段中,垂线段最短
∴BF即为PD+BP的最小值
∴BF与AD的交点即为P点,如下图所示
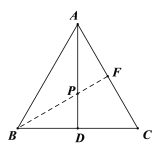
∵∠CAD=∠ABF=∠CBF =30°
∴AP= BP,PD=![]() BP=
BP=![]() AP
AP
∵AD=12
∴AP+PD=12
∴AP+![]() AP=12
AP=12
解得:AP=8
故选B.


 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案科目:初中数学 来源: 题型:
【题目】已知等腰三角形ABC,∠A是顶角,且∠A等于∠C的一半,BD是△ABC的角平分线,则该图中共有等腰三角形的个数是( )
A.4个B.3个C.2个D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,小兰用尺规作图作△ABC边AC上的高BH,作法如下:
①分别以点DE为圆心,大于DE的一半长为半径作弧两弧交于F;
②作射线BF,交边AC于点H;
③以B为圆心,BK长为半径作弧,交直线AC于点D和E;
④取一点K使K和B在AC的两侧;
所以BH就是所求作的高.其中顺序正确的作图步骤是( )

A.①②③④B.④③①②C.②④③①D.④③②①
查看答案和解析>>
科目:初中数学 来源: 题型:
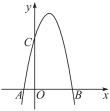
【题目】如图,一个二次函数的图象经过A,B,C三点,点A的坐标为(-1,0),点B的坐标为(4,0),点C在y轴的正半轴上,且AB=OC.
(1)求点C的坐标;
(2)求这个二次函数的解析式,并求出该函数的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据下列问题,列出关于![]() 的方程,并将其化成一元二次方程的一般形式.
的方程,并将其化成一元二次方程的一般形式.
(1)4个完全相同的正方形的面积之和是25,求正方形的边长![]() .
.
(2)一个矩形的长比宽多2,面积是100,求矩形的长![]() .
.
(3)一个直角三角形的斜边长为10,两条直角边相差2,求较长的直角边长![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O中,直径CD⊥弦AB于E,AM⊥BC于M,交CD于N,连接AD.
(1)求证:AD=AN;
(2)若AB=8,ON=1,求⊙O的半径.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题中错误的是( )
A. 圆柱的轴截面是过母线的截面中面积最大的一个
B. 圆锥的轴截面是所有过顶点的截面中面积最大的一个
C. 圆台的所有平行于底面的截面都是圆
D. 圆锥所有的轴截面是全等的等腰三角形
查看答案和解析>>
科目:初中数学 来源: 题型:
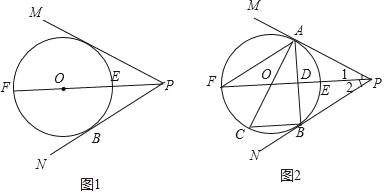
【题目】如图1,已知∠MPN的角平分线PF经过圆心O交⊙O于点E、F,PN是⊙O的切线,B为切点.
(1)求证:PM也是⊙O的切线;
(2)如图2,在(1)的前提下,设切线PM与⊙O的切点为A,连接AB交PF于点D;连接AO交⊙O于点C,连接BC,AF;记∠PFA为∠α.
①若BC=6,tan∠α=![]() ,求线段AD的长;
,求线段AD的长;
②小华探究图2之后发现:EF2=mODOP(m为正整数),请你猜想m的数值?并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中
中![]() ,
,![]() ,点
,点![]() 在
在![]() 边上,
边上,![]() 于点
于点![]() .
.

![]() 若
若![]() ,
,![]() ,求
,求![]() 的长;
的长;
![]() 设点
设点![]() 在线段
在线段![]() 上,点
上,点![]() 在射线
在射线![]() 上,以
上,以![]() ,
,![]() ,
,![]() 为顶点的三角形与
为顶点的三角形与![]() 有一个锐角相等,
有一个锐角相等,![]() 交
交![]() 于点
于点![]() .问:线段
.问:线段![]() 可能是
可能是![]() 的高线还是中线?或两者都有可能?请说明理由.
的高线还是中线?或两者都有可能?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com