【题目】如图所示，小兰用尺规作图作△ABC边AC上的高BH，作法如下：
①分别以点DE为圆心，大于DE的一半长为半径作弧两弧交于F；
②作射线BF，交边AC于点H；
③以B为圆心，BK长为半径作弧，交直线AC于点D和E；
④取一点K使K和B在AC的两侧；
所以BH就是所求作的高．其中顺序正确的作图步骤是（ ）
A.①②③④B.④③①②C.②④③①D.④③②①
冲刺100分单元优化练考卷系列答案科目：初中数学 来源： 题型：
【题目】为了促进节能减排，倡导节约用电，某市将实行居民生活用电阶梯电价方案，图中折线反映了每户每月用电电费y（元）与用电量x（度）间的函数关系式．
（1）根据图象，阶梯电价方案分为三个档次，填写下表：
档次 | 第一档 | 第二档 | 第三档 |
每月用电量x（度） | 0＜x≤140 |
（2）小明家某月用电120度，需交电费 元
（3）求第二档每月电费y（元）与用电量x（度）之间的函数关系式；
（4）在每月用电量超过230度时，每多用1度电要比第二档多付电费m元，小刚家某月用电290度，交电费153元，求m的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知：在△ABC中，AC=BC，∠ACB=90°，点D是AB的中点，点E是AB边上一点．
（1）直线BF垂直于直线CE于点F，交CD于点G（如图1），求证：AE=CG；
（2）直线AH垂直于直线CE，垂足为点H，交CD的延长线于点M（如图2），找出图中与BE相等的线段，并证明．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知：如图，一块Rt△ABC的绿地，量得两直角边AC=8cm，BC=6cm.现在要将这块绿地扩充成等腰△ABD，且扩充部分（△ADC）是以8cm为直角边长的直角三角形，求扩充等腰△ABD的周长.
（1）在图1中，当AB=AD=10cm时，△ABD的周长为 ．
（2）在图2中，当BA=BD=10cm时，△ABD的周长为 ．
（3）在图3中，当DA=DB时，求△ABD的周长.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，二次函数y=ax2+bx+c的图象过点A（3，0），对称轴为直线x=1，给出以下结论：①abc＜0；②b2﹣4ac＞0；③a+b+c≥ax2+bx+c；④若M（x2+1，y1）、N（x2+2，y2）为函数图象上的两点，则y1＜y2，其中正确的是（ ）
A. ①②③ B. ①②④ C. ①③④ D. ②③④
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图是用
个相同的小长方形与
个小正方形镶嵌而成的正方形图案，已知该图案的面积为
,小正方形的面积为
,若用
表示小长方形的两边长(
) ,请观察图案，指出以下关系式中,不正确的是（ ）
A.
B.
C.
D.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】抛物线y=﹣x2+bx+c与x轴交于A（﹣3，0），B（1，0）两点，与y轴交于点C．
（1）求该抛物线的解析式；
（2）在抛物线上求一点P，使S△PAB=S△ABC，写出P点的坐标；
（3）在抛物线的对称轴上是否存在点Q，使得△QBC的周长最小？若存在，求出点Q的坐标，若不存在，请说明理由．
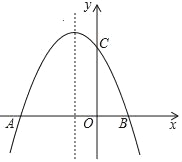
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】我们知道，有理数包括整数、有限小数和无限循环小数，事实上，所有的有理数都可以化为分数形式（整数可看作分母为1的分数），那么无限循环小数如何表示为分数形式呢？请看以下示例：
例：将
化为分数形式
由于=0.777…，设x=0.777…①
则10x=7.777…②
②﹣①得9x=7，解得x=
，于是得=．
同理可得
=
，
=1+
=1+
，
根据以上阅读，回答下列问题：（以下计算结果均用最简分数表示）
（基础训练）
（1）
= ，
= ；
（2）将
化为分数形式，写出推导过程；
（能力提升）
（3）
= ，
= ；
（注：=0.315315…，=2.01818…）
（探索发现）
（4）①试比较
与1的大小： 1（填“＞”、“＜”或“=”）
②若已知
=
，则
= ．
（注：=0.285714285714…）
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
