
【题目】如图,在![]() 中
中![]() ,
,![]() ,点
,点![]() 在
在![]() 边上,
边上,![]() 于点
于点![]() .
.

![]() 若
若![]() ,
,![]() ,求
,求![]() 的长;
的长;
![]() 设点
设点![]() 在线段
在线段![]() 上,点
上,点![]() 在射线
在射线![]() 上,以
上,以![]() ,
,![]() ,
,![]() 为顶点的三角形与
为顶点的三角形与![]() 有一个锐角相等,
有一个锐角相等,![]() 交
交![]() 于点
于点![]() .问:线段
.问:线段![]() 可能是
可能是![]() 的高线还是中线?或两者都有可能?请说明理由.
的高线还是中线?或两者都有可能?请说明理由.
【答案】(1)6;(2)见解析
【解析】
(1)根据已知条件易证DE∥BC,再由平行线分线段成比例定理列比例式即可求解;(2)分三种情况讨论:①若∠CFG=∠ECD,此时线段CP是△CFG的FG边上的中线;②若∠CFG=∠EDC,此时线段CP为△CFG的FG边上的高线;③当CD为∠ACB的平分线时,CP既是△CFG的FG边上的高线又是中线.
解:![]() ∵
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ;
;
![]() ①如图
①如图![]() ,若
,若![]() ,此时线段
,此时线段![]() 是
是![]() 的
的![]() 边上的中线.
边上的中线.
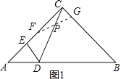
证明:∵![]() ,
,![]() ,
,
又∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴线段![]() 是
是![]() 的
的![]() 边上的中线;
边上的中线;
②如图![]() ,若
,若![]() ,此时线段
,此时线段![]() 为
为![]() 的
的![]() 边上的高线.
边上的高线.

证明:∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴线段![]() 为
为![]() 的
的![]() 边上的高线.
边上的高线.
③如图![]() ,当
,当![]() 为
为![]() 的平分线时,
的平分线时,![]() 既是
既是![]() 的
的![]() 边上的高线又是中线.
边上的高线又是中线.


科目:初中数学 来源: 题型:
【题目】我们知道,有理数包括整数、有限小数和无限循环小数,事实上,所有的有理数都可以化为分数形式(整数可看作分母为1的分数),那么无限循环小数如何表示为分数形式呢?请看以下示例:
例:将![]() 化为分数形式
化为分数形式
由于![]() =0.777…,设x=0.777…①
=0.777…,设x=0.777…①
则10x=7.777…②
②﹣①得9x=7,解得x=![]() ,于是得
,于是得![]() =
=![]() .
.
同理可得![]() =
=![]() ,
,![]() =1+
=1+![]() =1+
=1+![]() ,
,
根据以上阅读,回答下列问题:(以下计算结果均用最简分数表示)
(基础训练)
(1)![]() = ,
= ,![]() = ;
= ;
(2)将![]() 化为分数形式,写出推导过程;
化为分数形式,写出推导过程;
(能力提升)
(3)![]() = ,
= ,![]() = ;
= ;
(注:![]() =0.315315…,
=0.315315…,![]() =2.01818…)
=2.01818…)
(探索发现)
(4)①试比较![]() 与1的大小:
与1的大小:![]() 1(填“>”、“<”或“=”)
1(填“>”、“<”或“=”)
②若已知![]() =
=![]() ,则
,则![]() = .
= .
(注:![]() =0.285714285714…)
=0.285714285714…)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:在平面直角坐标系xOy中,对于任意两点P1(x1,y1)与P2(x2,y2)的“非常距离”,给出如下定义:
若|x1﹣x2|≥|y1﹣y2|,则点P1与点P2的“非常距离”为|x1﹣x2|;
若|x1﹣x2|<|y1﹣y2|,则点P1与点P2的“非常距离”为|y1﹣y2|.
例如:点P1(1,1),点P2(2,3),因为|1﹣2|<|1﹣3|,所以点P1与点P2的“非常距离”为|1﹣3|=2,也就是图1中线段P1Q与线段P2Q长度的较大值(点Q为垂直于y轴的直线P1Q与垂直于x轴的直线P2Q的交点).
(1)已知点A(-![]() ,0),B为y轴上的一个动点.
,0),B为y轴上的一个动点.
①若点B(0,3),则点A与点B的“非常距离”为______;
②若点A与点B的“非常距离”为2,则点B的坐标为_______;
③直接写出点A与点B的“非常距离”的最小值为_______;
(2)已知点D(0,1),点C是直线y=﹣![]() x+3上的一个动点,如图2,求点C与点D“非常距离”的最小值及相应的点C的坐标.
x+3上的一个动点,如图2,求点C与点D“非常距离”的最小值及相应的点C的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:四边形ABCD的对角线AC,BD相交于点O,给出下列4个条件:①AB∥CD;②OA=OC;③AB=CD;④AD∥BC.从中任取两个条件,能推出四边形ABCD是平行四边形的概率是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,AE平分∠BAC交BC于点E,O是AB上一点,经过A,E两点的⊙O交AB于点D,连接DE,作∠DEA的平分线EF交⊙O于点F,连接AF.
(1)求证:BC是⊙O的切线;
(2)若sin∠EFA=![]() ,AF=
,AF=![]() ,求线段AC的长.
,求线段AC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面的材料,回答问题:
解方程![]() ,这是一个一元四次方程,根据该方程的特点,它的解法通常是:
,这是一个一元四次方程,根据该方程的特点,它的解法通常是:
设![]() ,那么
,那么![]() ,于是原方程可变为
,于是原方程可变为![]() ①,解得
①,解得![]() ,
,![]() .
.
当![]() 时,
时,![]() ,∴
,∴![]() ;
;
当![]() 时,
时,![]() ,∴
,∴![]() ;
;
∴原方程有四个根:![]() ,
,![]() ,
,![]() ,
,![]() .
.
![]() 在由原方程得到方程①的过程中,利用________法达到________的目的,体现了数学的转化思想.
在由原方程得到方程①的过程中,利用________法达到________的目的,体现了数学的转化思想.
![]() 解方程
解方程![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com