
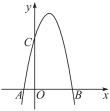
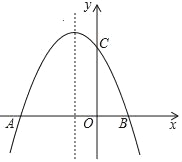
【题目】如图,一个二次函数的图象经过A,B,C三点,点A的坐标为(-1,0),点B的坐标为(4,0),点C在y轴的正半轴上,且AB=OC.
(1)求点C的坐标;
(2)求这个二次函数的解析式,并求出该函数的最大值.
【答案】(1)点C的坐标为(0,5);(2)所求二次函数的解析式为y=-![]() x2+
x2+![]() x+5,最大值为
x+5,最大值为![]() .
.
【解析】
(1)根据A.B两点的坐标及点C在y轴正半轴上,且AB=OC.求出点C的坐标为(0,5);
(2)设二次函数的解析式为y=ax2+bx+c,把A、B、C三点的坐标代入解析式,可求出a、b、c的值.
(1)∵A(-1,0),B(4,0)
∴AO=1,OB=4,
AB=AO+OB=1+4=5,
∴OC=5,即点C的坐标为(0,5);
(2)设图象经过A、C、B三点的二次函数的解析式为y=ax2+bx+c
由于这个函数图象过点(0,5),可以得到C=5,又由于该图象过点(-1,0),(4,0),则:
![]() ,
,
解方程组,得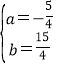
∴所求的函数解析式为y=-![]() x2+
x2+![]() x+5
x+5
∵a=-![]() <0
<0
∴当x=-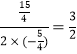 时,y有最大值
时,y有最大值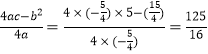 .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】已知A组数据为2、3、6、6、7、8、8、8,B组数据为4、5、8、8、9、10、10、10,则描述A、B两组数据的统计量中相等的是( )
A. 众数 B. 中位数 C. 平均数 D. 方差
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,一块Rt△ABC的绿地,量得两直角边AC=8cm,BC=6cm.现在要将这块绿地扩充成等腰△ABD,且扩充部分(△ADC)是以8cm为直角边长的直角三角形,求扩充等腰△ABD的周长.
(1)在图1中,当AB=AD=10cm时,△ABD的周长为 .
(2)在图2中,当BA=BD=10cm时,△ABD的周长为 .
(3)在图3中,当DA=DB时,求△ABD的周长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是用![]() 个相同的小长方形与
个相同的小长方形与![]() 个小正方形镶嵌而成的正方形图案,已知该图案的面积为
个小正方形镶嵌而成的正方形图案,已知该图案的面积为![]() ,小正方形的面积为
,小正方形的面积为![]() ,若用
,若用![]() 表示小长方形的两边长(
表示小长方形的两边长(![]() ) ,请观察图案,指出以下关系式中,不正确的是( )
) ,请观察图案,指出以下关系式中,不正确的是( )

A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=﹣x2+bx+c与x轴交于A(﹣3,0),B(1,0)两点,与y轴交于点C.
(1)求该抛物线的解析式;
(2)在抛物线上求一点P,使S△PAB=S△ABC,写出P点的坐标;
(3)在抛物线的对称轴上是否存在点Q,使得△QBC的周长最小?若存在,求出点Q的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某园林专业户计划投资种植花卉及树木,根据市场调查与预测,种植树木的利润y1与投资量x成正比例关系,种植花卉的利润y2与投资量x的平方成正比例关系,并得到了表格中的数据.
投资量x(万元) | 2 |
种植树木利润y1(万元) | 4 |
种植花卉利润y2(万元) | 2 |
(1)分别求出利润y1与y2关于投资量x的函数关系式;
(2)如果这位专业户以8万元资金投入种植花卉和树木,设他投入种植花卉金额m万元,种植花卉和树木共获利利润W万元,直接写出W关于m的函数关系式,并求他至少获得多少利润?他能获取的最大利润是多少?
(3)若该专业户想获利不低于22万,在(2)的条件下,直接写出投资种植花卉的金额m的范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于多项式Ax2bxc(b、c为常数),作如下探究:
(1)不论x取何值,A都是非负数,求b与c满足的条件;
(2)若A是完全平方式,
①当c=9时,b= ;当b=3时,c= ;
②若多项式Bx2dxc与A有公因式,求d的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com