【题目】某商场试销一种成本为8元/千克的水果，经试销发现，销量y（千克）与销售单价x（元）符合一次函数y=kx+b，且当x=10时，y=300；当x=13时，y=150．
（1）求y（千克）与x（元）（x＞8）的函数关系式；
（2）设该超市销售这种水果每天获取的利润为W元，那么当销售单价为何值时，每天可获得的利润最大？最大利润是多少元？
科目：初中数学 来源： 题型：
【题目】2019年是中国建国70周年，作为新时期的青少年，我们应该肩负起实现祖国伟大复兴的责任，为了培养学生的爱国主义情怀，我校学生和老师在5月下旬集体乘车去抗日战争纪念馆研学，已知学生的人数是老师人数的12倍多20人，学生和老师总人数有540人．
（1）请求出去抗日战争纪念馆研学的学生和老师的人数各是多少？
（2）如果学校准备租赁
型车和
型车共14辆（其中型车最多7辆），已知型车每年最车可以载35人，型车每车最多可以载45人，共有几种租车方案？
（3）已知型车日租金为2000元，型车日租金为3000元，设租赁型大巴车
辆，求出租赁总租金为
元与的函数解析式，并求出最经济的租车方案．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在边长为4的正方形ABCD中，E、F是AD边上的两个动点，且AE=FD，连接BE、CF、BD，CF与BD交于点G，连接AG交BE于点H，连接DH，下列结论正确的个数是（ ）
①△ABG∽△FDG ②HD平分∠EHG ③AG⊥BE ④S△HDG：S△HBG=tan∠DAG ⑤线段DH的最小值是2 
﹣2．
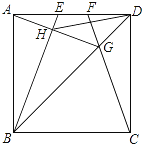
A. 2 B. 3 C. 4 D. 5
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知点P（﹣2，3）是反比例函数y=
图象上的一点，则下列各点中，也在该函数图象上的是（ ）
A. （2，﹣3） B. （3，2） C. （﹣2，﹣3） D. （2，3）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】今年5月，某大型商业集团随机抽取所属的部分商业连锁店进行评估，将抽取的各商业连锁店按照评估成绩分成了
、
、
、
四个等级，并绘制了如下不完整的扇形统计图和条形统计图.
根据以上信息，解答下列问题：
（1）本次评估随机抽取了多少家商业连锁店？
（2）请补充完整扇形统计图和条形统计图，并在图中标注相应数据；
（3）从、两个等级的商业连锁店中任选2家介绍营销经验，求其中至少有一家是等级的概率.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】小赵投资销售一种进价为每件20元的护眼台灯．销售过程中发现,当月内销售单价不变,则月销售量y（件）与销售单价x（元）之间的关系可近似的看作一次函数：
．
(1)设小赵每月获得利润为w（元）,当销售单价定为多少元时,每月可获得最大利润？并求出最大利润.
(2)如果小赵想要每月获得的利润不低于2000元,那么如何制定销售单价才可以实现这一目标？
查看答案和解析>>
科目：初中数学 来源： 题型：
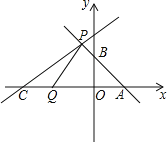
【题目】如图，直线l1：y1＝﹣x+2与x轴，y轴分别交于A，B两点，点P(m，3)为直线l1上一点，另一直线l2：y2＝
x+b过点P．
（1）求点P坐标和b的值；
（2）若点C是直线l2与x轴的交点，动点Q从点C开始以每秒1个单位的速度向x轴正方向移动．设点Q的运动时间为t秒；
①请写出当点Q在运动过程中，△APQ的面积S与t的函数关系式；
②直接写出当t为何值时△APQ的面积等于4.5，并写出此时点Q的坐标．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
