
【题目】2019年是中国建国70周年,作为新时期的青少年,我们应该肩负起实现祖国伟大复兴的责任,为了培养学生的爱国主义情怀,我校学生和老师在5月下旬集体乘车去抗日战争纪念馆研学,已知学生的人数是老师人数的12倍多20人,学生和老师总人数有540人.
(1)请求出去抗日战争纪念馆研学的学生和老师的人数各是多少?
(2)如果学校准备租赁![]() 型车和
型车和![]() 型车共14辆(其中
型车共14辆(其中![]() 型车最多7辆),已知
型车最多7辆),已知![]() 型车每年最车可以载35人,
型车每年最车可以载35人,![]() 型车每车最多可以载45人,共有几种租车方案?
型车每车最多可以载45人,共有几种租车方案?
(3)已知![]() 型车日租金为2000元,
型车日租金为2000元,![]() 型车日租金为3000元,设租赁
型车日租金为3000元,设租赁![]() 型大巴车
型大巴车![]() 辆,求出租赁总租金为
辆,求出租赁总租金为![]() 元与
元与![]() 的函数解析式,并求出最经济的租车方案.
的函数解析式,并求出最经济的租车方案.
【答案】(1)去抗日战争纪念馆研学的学生有500人,老师有40人;(2)3;(3)租赁A型大巴车9辆和租赁B型大巴车5辆.
【解析】
(1)设去参观抗日战争纪念馆学生有x人,老师有y人,根据题意,得出关于x,y的二元一次方程组,解之即可得出结论;
(2)设租赁B型大巴车m辆,则租赁A型大巴车(14-m)辆,由B型大巴车最多有7辆及租赁的14辆车至少能坐下540人,即可得出关于m的一元一次不等式组,解之即可得出m的取值范围,结合m为正整数即可得出m的值,从而得到租车方案;
(3)设租赁总租金为w元,根据总租金=每辆车的租金金额×租车辆数,即可得出w关于m的函数关系式,再利用一次函数的性质即可找出最经济的租赁车辆方案.
解:(1)设去去抗日战争纪念馆研学的学生有x人,老师有y人,
依题意,得:
![]() ,解得:
,解得:![]() .
.
答:去抗日战争纪念馆研学的学生有500人,老师有40人.
(2)设租赁B型大巴车m辆,则租赁A型大巴车(14-m)辆,
依题意,得:
![]() ,
,
解得:5≤m≤7.
∵m为正整数,
∴m=5,6或7.
∴租车方案有3种:①租A型车9辆,B型车5辆;②租A型车8辆,B型车6辆;③租A型车7辆,B型车7辆;
(3)设租赁总租金为w元,依题意,得:
w=3000m+2000(14-m)=1000m+28000,
∵1000>0,
∴w的值随m值的增大而增大,
∴当m=5时,w取得最小值,
∴最经济的租赁车辆方案为:租赁A型大巴车9辆和租赁B型大巴车5辆.


 导学全程练创优训练系列答案
导学全程练创优训练系列答案科目:初中数学 来源: 题型:
【题目】某市为了解本地七年级学生寒假期间参加社会实践活动情况,随机抽查了部分七年级学生寒假参加社会实践活动的天数(“A﹣﹣﹣不超过5天”、“B﹣﹣﹣6天”、“C﹣﹣﹣7天”、“D﹣﹣﹣8天”、“E﹣﹣﹣9天及以上”),并将得到的数据绘制成如下两幅不完整的统计图.
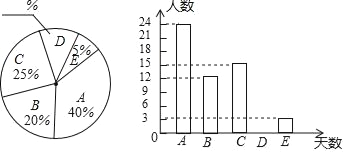
请根据以上的信息,回答下列问题:
(1)补全扇形统计图和条形统计图;
(2)所抽查学生参加社会实践活动天数的众数是 (选填:A、B、C、D、E);
(3)若该市七年级约有2000名学生,请你估计参加社会实践“活动天数不少于7天”的学生大约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:一个自然数,右边的数字总比左边的数字小,我们称它为“下滑数”(如:32,641,8531等).现从两位数中任取一个,恰好是“下滑数”的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形网格中,每个小正方形的边长都为1,点A,点B在网格中的位置如图所示.
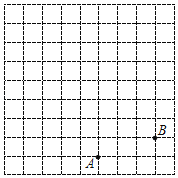
(1)建立适当的直角坐标系,使点A,点B的坐标分别为(1,﹣3),(4,﹣2);
(2)若点C的坐标为(﹣1,﹣1),在平面直角坐标系中画出△ABC;
(3)在图中作出△ABC关于x轴对称的图形△A1B1C1.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数![]() 的图象与y轴交于点A,点B(-1,n)是该函数图象与反比例函数
的图象与y轴交于点A,点B(-1,n)是该函数图象与反比例函数![]() (k≠0)图象在第二象限内的交点.
(k≠0)图象在第二象限内的交点.
(1)求点B的坐标及k的值;
(2)试在x轴上确定点C,使AC=AB,请直接写出点C的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解学生体质情况,从各年级学生中随机抽取部分学生进行体能测试.
每个学生的测试成绩按标准对应为优秀、良好、及格、不及格四个等级.统计员在将测试数据绘制 成图表时发现,优秀漏统计4人,良好漏统计6人,于是及时更正,从而形成如下图表.请按正确数据解答下列各题:
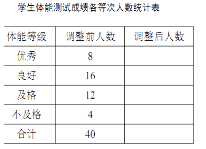
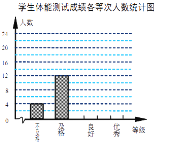
(1)填写统计表.
(2)根据调整后数据,补全条形统计图.
(3)若该校共有学生1500人,请你估算出该校体能测试等级为“优秀”的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场试销一种成本为8元/千克的水果,经试销发现,销量y(千克)与销售单价x(元)符合一次函数y=kx+b,且当x=10时,y=300;当x=13时,y=150.
(1)求y(千克)与x(元)(x>8)的函数关系式;
(2)设该超市销售这种水果每天获取的利润为W元,那么当销售单价为何值时,每天可获得的利润最大?最大利润是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com