
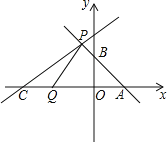
【题目】如图,直线l1:y1=﹣x+2与x轴,y轴分别交于A,B两点,点P(m,3)为直线l1上一点,另一直线l2:y2=![]() x+b过点P.
x+b过点P.
(1)求点P坐标和b的值;
(2)若点C是直线l2与x轴的交点,动点Q从点C开始以每秒1个单位的速度向x轴正方向移动.设点Q的运动时间为t秒;
①请写出当点Q在运动过程中,△APQ的面积S与t的函数关系式;
②直接写出当t为何值时△APQ的面积等于4.5,并写出此时点Q的坐标.
【答案】(1)P的坐标为(﹣1,3),b=![]() ;(2)①S=
;(2)①S=![]() (0<t<9)或S=
(0<t<9)或S=![]() (t>9);②Q的坐标为(﹣1,0)或(5,0).
(t>9);②Q的坐标为(﹣1,0)或(5,0).
【解析】
(1)把P(m,3)的坐标代入直线l1上的解析式即可求得P的坐标,然后根据待定系数法即可求得b;
(2)根据直线l2的解析式得出C的坐标,①根据题意得出AQ=9﹣t,然后根据S=![]() AQ|yP|即可求得△APQ的面积S与t的函数关系式;②通过解方程﹣
AQ|yP|即可求得△APQ的面积S与t的函数关系式;②通过解方程﹣![]() t+
t+![]() =4.5或
=4.5或![]() t﹣
t﹣![]() =4.5,求得t的值,即可求得Q的坐标.
=4.5,求得t的值,即可求得Q的坐标.
解:(1)∵点P(m,3)为直线l1上一点,
∴3=﹣m+2,解得m=﹣1,
∴点P的坐标为(﹣1,3),
把点P的坐标代入y2=![]() x+b得,3=
x+b得,3=![]() ×(﹣1)+b,
×(﹣1)+b,
解得b=![]() ;
;
(2)∵直线l2的解析式为y=![]() x+
x+![]() ,
,
∴C点的坐标为(﹣7,0),
①由直线l1:y1=﹣x+2可知A(2,0),
∴当Q在A、C之间时,AQ=2+7﹣t=9﹣t(0<t<9),
∴S=![]() AQ|yP|=
AQ|yP|=![]() ×(9﹣t)×3=
×(9﹣t)×3=![]() ﹣
﹣![]() t;
t;
当Q在A的右边时,AQ=t﹣9(t>9),
∴S=![]() AQ|yP|=
AQ|yP|=![]() ×(t﹣9)×3=
×(t﹣9)×3=![]() t﹣
t﹣![]() ;
;
即△APQ的面积S与t的函数关系式为S=﹣![]() t+
t+![]() (0<t<9)或S=
(0<t<9)或S=![]() t﹣
t﹣![]() (t>9);
(t>9);
②∵S=4.5,
∴﹣![]() t+
t+![]() =4.5或
=4.5或![]() t﹣
t﹣![]() =4.5
=4.5
解得t=6或t=12,
∴Q的坐标为(﹣1,0)或(5,0).


科目:初中数学 来源: 题型:
【题目】某商场试销一种成本为8元/千克的水果,经试销发现,销量y(千克)与销售单价x(元)符合一次函数y=kx+b,且当x=10时,y=300;当x=13时,y=150.
(1)求y(千克)与x(元)(x>8)的函数关系式;
(2)设该超市销售这种水果每天获取的利润为W元,那么当销售单价为何值时,每天可获得的利润最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在平面直角坐标系内,△ABC各顶点的坐标分别是A(﹣2,4),B(﹣4,3),C(﹣1,1).将△ABC向右平移5个单位长度,再向下平移4个单位长度得到△A′B′C′.
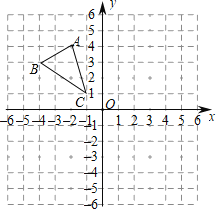
(1)请作出平移后的△A′B′C′,并写出△A′B′C′各顶点的坐标;
(2)如果将△A′B′C′看成是由△ABC经过一次平移得到的,请指出这一平移的平移方向和平移距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AD=3,CD=4,点P是AC上一个动点(点P与点A,C不重合),过点P分别作PE⊥BC于点E,PF∥BC交AB于点F,连接EF,则EF的最小值为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
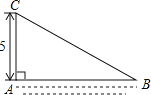
【题目】如图所示,在离水面高度5米的岸上有人用绳子拉船靠岸,开始时绳子BC的长度为13米,此人以每秒0.5米的速度收绳.问:
(1)未开始收绳的时候,图中船B距岸A的长度AB是多少米?
(2)收绳10秒后船向岸边移动了多少米?(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边△ABC的边长是2,D、E分别为AB、AC的中点,延长BC至点F,使CF=![]() BC,连接CD和EF.
BC,连接CD和EF.

(1)求证:DE=CF;
(2)求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为宣传“扫黑除恶”专项行动,社区准备制作一幅宣传版面,喷绘时为了美观,要在矩形图案四周外围增加一圈等宽的白边,已知图案的长为2米,宽为1米,图案面积占整幅宣传版面面积的90%,若设白边的宽为x米,则根据题意可列出方程( )

A. 90%×(2+x)(1+x)=2×1 B. 90%×(2+2x)(1+2x)=2×1
C. 90%×(2﹣2x)(1﹣2x)=2×1 D. (2+2x)(1+2x)=2×1×90%
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,斜边
中,斜边![]() 的中垂线
的中垂线![]() 交
交![]() 于点
于点![]() ,交
,交![]() 的外角平分线于点
的外角平分线于点![]() ,
,![]() 于点
于点![]() ,
,![]() 垂直
垂直![]() 的延长线与点
的延长线与点![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() ,现有不列结论:①
,现有不列结论:①![]() ,②
,②![]() ,③
,③![]() ,④
,④![]() ,⑤
,⑤![]() ,其中正确的个数是( )
,其中正确的个数是( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题提出:将一个边长为n(n≥2)的正三角形的三条边n等分,连接各边对应的等分点, 则该三角形被剖分的网格中的结点个数和线段数分别是多少呢?
问题探究:要研究上面的问题,我们不妨先从特例入手,进而找到一般规律
探究一:将一个边长为2的正三角形的三条边平分,连接各边中点,则该三角形被剖分的网格中的结点个数和线段数分别是多少?
如图1,连接边长为2的正三角形三条边的中点,从上往下:共有1+2+3=6个结点.边长为1的正三角形,第一层有1个,第二层有2个,共有1+2=3个,线段数为3×3=9条;边长为2的正三角形有1个,线段数为3条,总共有3×(1+2+1)=2×(1+2+3)=12条线段.

探究二:将一个边长为3的正三角形的三条边三等分,连接各边对应的等分点,则该三角形被剖分的网格中的结点个数和线段数分别是多少?
如图2,连接边长为3的正三角形三条边的对应三等分点,从上往下:共有1+2+3+4=10个结点.边长为1的正三角形,第一层有1个,第二层有2个,第三层有3个,共有1+2+3=6个,线段数为3×6=18条;边长为2的正三角形有1+2=3个,线段数为3×3=9条,边长为3的正三角形有1个,线段数为3条,总共有3×(1+2+3+1+2+1)=3×(1+2+3+4)=30条线段.
探究三:
请你仿照上面的方法,探究将边长为4的正三角形的三条边四等分(图3),连接各边对应的等分点,该三角形被剖分的网格中的结点个数和线段数分别是多少?
(画出示意图,并写出探究过程)
问题解决:
请你仿照上面的方法,探究将一个边长为n(n≥2)的正三角形的三条边n等分,连接各边对应的等分点,则该三角形被剖分的网格中的结点个数和线段数分别是多少?(写出探究过程)
实际应用:
将一个边长为30的正三角形的三条边三十等分,连接各边对应的等分点,则该三角形被剖分的网格中的结点个数和线段数分别是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com