
【题目】我们把按一定规律排列的一列数称为数列,若对于一个数列中任意相邻有序的三个数![]() ,
,![]() ,
,![]() ,总满足
,总满足![]() ,则称这个数列为理想数列.
,则称这个数列为理想数列.
(1)在数列①![]() ,
,![]() ,
,![]() ,
,![]() ;②3,-2,-1,1中,是理想数列的是______(只填序号即可)
;②3,-2,-1,1中,是理想数列的是______(只填序号即可)
(2)如果数列![]() ,是理想数列,求
,是理想数列,求![]() 的值;
的值;
(3)若数列![]() ,是理想数列,求代数式
,是理想数列,求代数式![]() 的值;
的值;
(4)请写出一个由五个不同正整数组成的理想数列:______.
【答案】(1)②;(2)![]() ;(3)-1;(4)2,3,5,13,57.
;(3)-1;(4)2,3,5,13,57.
【解析】
(1)根据理想数列的定义进行判断即可;
(2)根据理想数列的定义列出方程,解方程即可;
(3)根据理想数列的定义列出方程:![]() ,整理出式子:
,整理出式子:![]() ,代入
,代入![]() 进行计算即可;
进行计算即可;
(4)先确定第一个数为2,第二个数为3,依据理想数列的定义找到第三、四、五个数即可.
解:(1)①![]() ,
,![]() ,
,![]() ,
,![]() 中:后面三个数值的关系为:
中:后面三个数值的关系为: ![]() ,故①不是理想数列;
,故①不是理想数列;
②3,-2,-1,1中:![]() 及
及![]() ,故②是理想数列;
,故②是理想数列;
故答案为:②
(2)根据题意得![]() ,
,
解得![]() .
.
(3)因为数列![]() ,是理想数列
,是理想数列
所以![]() ,
,
所以![]() ,
,
所以![]()
![]()
![]() .
.
(4)设第一个数为2,第二个数为3,则第三个数为:![]()
则第四个数为:![]()
则第五个数为:![]()
故答案为:2,3,5,13,57


 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案科目:初中数学 来源: 题型:
【题目】将若干个奇数按每行8个数排成如图的形式:
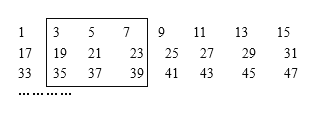
小军画了一方框框住了其中的9个数.
(1)如图中方框内9个数之和是 ;
(2)若小军画的方框内9个数之和等于333,则这个方框内左下角的那个数为_________;
(3)试说明:方框内的9个数之和总是9的倍数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算下列各题
(1)﹣2+(﹣7)+8.
(2)25﹣13﹣4﹣25.
(3)![]() .
.
(4)(﹣2.4)﹣(﹣4.5)+|﹣2.4|+(﹣0.5).
(5)(![]() )×(﹣36).
)×(﹣36).
(6)![]() .
.
(7)![]() ×(﹣12).
×(﹣12).
(8)13×(﹣![]() )+(﹣13)×
)+(﹣13)×![]() +13×
+13×![]() .
.
(9)﹣12018+![]() .
.
(10)![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
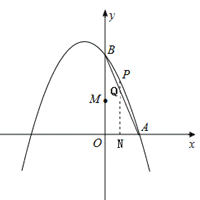
【题目】如图,已知抛物线经过A(1,0),B(0,3)两点,对称轴是直线x=﹣1.
(1)求抛物线对应的函数关系式;
(2)点N在线段OA上,点M在线段OB上,且OM=2ON,过点N作x轴的垂线交线段AB于点Q,交抛物线于点P.
①当ON为何值时,四边形OMPN为矩形;
②△AOQ能否为等腰三角形?若能,求出此时ON的值;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数轴上,我们把表示数2的点定为核点,记作点![]() ,对于两个不同的点
,对于两个不同的点![]() 和
和![]() ,若点
,若点![]() ,
,![]() 到点
到点![]() 的距离相等,则称点
的距离相等,则称点![]() 与点
与点![]() 互为核等距点.如图,点
互为核等距点.如图,点![]() 表示数-1,点
表示数-1,点![]() 表示数5,它们与核点
表示数5,它们与核点![]() 的距离都是3个单位长度,我们称点
的距离都是3个单位长度,我们称点![]() 与点
与点![]() 互为核等距点.
互为核等距点.
![]()
(1)已知点![]() 表示数3,如果点
表示数3,如果点![]() 与点
与点![]() 互为核等距点,那么点
互为核等距点,那么点![]() 表示的数是______;
表示的数是______;
(2)已知点![]() 表示数
表示数![]() ,点
,点![]() 与点
与点![]() 互为核等距点,
互为核等距点,
①如果点![]() 表示数
表示数![]() ,求
,求![]() 的值;
的值;
②对点![]() 进行如下操作:先把点
进行如下操作:先把点![]() 表示的数乘以2,再把所得数表示的点沿着数轴向左移动5个单位长度得到点
表示的数乘以2,再把所得数表示的点沿着数轴向左移动5个单位长度得到点![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直接写出结果
(1)﹣7﹣3=
(2)2.5-(-3.5)=
(3)![]() -1=
-1=
(4)![]() ÷(﹣2)=
÷(﹣2)=
(5)﹣(﹣5)2=
(6)|+7|﹣|﹣5|=
(7)- 3xy-4xy ﹦
(8)3x-2![]() +3
+3![]() ﹦
﹦
(9)![]() +
+![]() ﹦
﹦
(10)6![]() -5
-5![]() ﹦
﹦
查看答案和解析>>
科目:初中数学 来源: 题型:
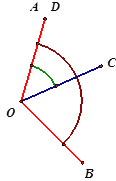
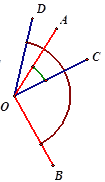
【题目】如图,已知,OA、OD重合,AOB=120,COD=50,当AOB绕点O顺时针旋转到AO与CO重合的过程中,下列结论正确的是( )
①OB旋转50②当OA平分COD时,BOC=95,③DOB+AOC=170,④BOC-AOD=70
A. ①②③ B. ②③④ C. ①③④ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,DB∥AC,且DB=![]() AC,E是AC的中点,
AC,E是AC的中点,
(1)求证:BC=DE;
(2)连接AD、BE,若要使四边形DBEA是矩形,则给△ABC添加什么条件,为什么?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将带有45°和30°两块直角三角尺的直角顶点C叠放在一起,
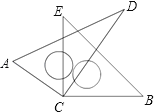
(1)若∠DCE=25°,则∠ACB=______;若∠ACB=150°,则∠DCE=______;
(2)猜想∠ACB与∠DCE的大小有何特殊关系,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com