
【题目】计算下列各题
(1)﹣2+(﹣7)+8.
(2)25﹣13﹣4﹣25.
(3)![]() .
.
(4)(﹣2.4)﹣(﹣4.5)+|﹣2.4|+(﹣0.5).
(5)(![]() )×(﹣36).
)×(﹣36).
(6)![]() .
.
(7)![]() ×(﹣12).
×(﹣12).
(8)13×(﹣![]() )+(﹣13)×
)+(﹣13)×![]() +13×
+13×![]() .
.
(9)﹣12018+![]() .
.
(10)![]() .
.
【答案】(1)-1;(2)-17;(3)![]() ;(4)4;(5)3;(6)﹣
;(4)4;(5)3;(6)﹣![]() ;(7)-1199;(8)-26;(9)2;(10)-24.
;(7)-1199;(8)-26;(9)2;(10)-24.
【解析】
(1)原式利用加法法则计算即可求出值;
(2)原式结合后,相加即可求出值;
(3)原式利用除法法则计算即可求出值;
(4)原式利用减法法则变形,计算即可求出值;
(5)原式利用乘法分配律计算即可求出值;
(6)原式先计算括号中的运算,再计算乘除运算即可求出值;
(7)原式变形后,利用乘法分配律计算即可求出值;
(8)原式逆用乘法分配律计算即可求出值;
(9)原式先计算乘方运算,再计算乘除运算,最后算就原式即可求出值;
(10)原式先计算乘方运算,再计算乘除运算,最后算加减运算即可求出值.
(1)原式=﹣9+8=﹣1;
(2)原式=﹣17;
(3)原式=![]() ×
×![]() =
=![]() ;
;
(4)原式=﹣2.4+2.4+4.5﹣0.5=4;
(5)原式=﹣6+24﹣15=3;
(6)原式=﹣![]() ×
×![]() ×
×![]() =﹣
=﹣![]() ;
;
(7)原式=(100﹣![]() )×(﹣12)=﹣1200+1=﹣1199;
)×(﹣12)=﹣1200+1=﹣1199;
(8)原式=13×(﹣![]() ﹣
﹣![]() +
+![]() )=13×(﹣2)=﹣26;
)=13×(﹣2)=﹣26;
(9)原式=![]()
(10)原式=﹣![]() ×24﹣
×24﹣![]() ×(﹣8)﹣25=﹣1+2﹣25=﹣24.
×(﹣8)﹣25=﹣1+2﹣25=﹣24.


科目:初中数学 来源: 题型:
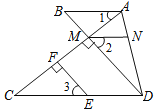
【题目】如图,已知:EF⊥AC,垂足为点F,DM⊥AC,垂足为点M,DM的延长线交AB于点B,且∠1=∠C,点N在AD上,且∠2=∠3,试说明AB∥MN.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对任意一个正整数m,如果m=k(k+1),其中k是正整数,则称m为“矩数”,k 为m的最佳拆分点.例如,56=7×(7+1),则56是一个“矩数”,7为56的最佳拆分点.
(1)求证:若“矩数”m是3的倍数,则m一定是6的倍数;
(2)把“矩数”p与“矩数”q的差记为 D(p,q),其中p>q,D(p,q)>0.例如,20=4×5,6=2×3,则 D(20,6)=20﹣6=14.若“矩数”p的最佳拆分点为t,“矩数”q的最佳拆分点为s,当 D(p,q)=30时,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
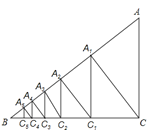
【题目】如图,已知Rt△ABC中,∠ACB=90°,AC=6,BC=8,过直角顶点C作CA1⊥AB,垂足为A1,再过A1作A1C1⊥BC,垂足为C1,过C1作C1A2⊥AB,垂足为A2,再过A2作A2C2⊥BC,垂足为C2,…,这样一直作下去,得到了一组线段CA1,A1C1,C1A2,A2C2,…,AnCn,则A1C1=_________,AnCn=__________ .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有小岛A和小岛B,轮船以45km/h的速度由C向B航行,在C处测得A的方位角为北偏东60°,测得B的方位角为南偏东45°,轮船航行2小时后到达小岛B处,在B处测得小岛A在小岛B的正北方向.求小岛A与小岛B之间的距离(结果保留整数,参考数据: ![]() ≈1.41,
≈1.41, ![]() ≈2.45)
≈2.45)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现在的青少年由于沉迷电视、手机、网络游戏,视力日渐减退,重庆某校九年级一班班主任为了了解可能影响学生视力下降的原因,对本班进行了一个“最喜爱的娱乐”调查,每个学生在A(看电视)、B(玩手机)、C(玩网络游戏)、D(其它)四种类型中只能选一项,并根据调查结果绘制成如下两幅不完整的统计图,请根据这两幅统计图解答下列问题:
(1)扇形统计图中C所占的百分比为 ,该班学生由于玩网络游戏而视力下降的学生有 人.
(2)为了让学生深刻认识保护视力的重要性,学校组织“保护视力 健康人生”的演讲比赛,班主任从选择D类型的学生中随机抽选两名学生参加比赛.已知D类型中有女生3人,其余的为男生.请求出刚好抽到的学生全部为女生的概率.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们把按一定规律排列的一列数称为数列,若对于一个数列中任意相邻有序的三个数![]() ,
,![]() ,
,![]() ,总满足
,总满足![]() ,则称这个数列为理想数列.
,则称这个数列为理想数列.
(1)在数列①![]() ,
,![]() ,
,![]() ,
,![]() ;②3,-2,-1,1中,是理想数列的是______(只填序号即可)
;②3,-2,-1,1中,是理想数列的是______(只填序号即可)
(2)如果数列![]() ,是理想数列,求
,是理想数列,求![]() 的值;
的值;
(3)若数列![]() ,是理想数列,求代数式
,是理想数列,求代数式![]() 的值;
的值;
(4)请写出一个由五个不同正整数组成的理想数列:______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知EF∥AD,∠1=∠2,∠BAC=70°,求∠AGD(请填空)

解:∵EF∥AD
∴∠2= (
又∵∠1=∠2
∴∠1=∠3( )
∴AB∥ ( )
∴∠BAC+ =180°( )
∵∠BAC=70°( )
∴∠AGD= ( )
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com