
【题目】如图,分别过点P作直线AB的垂线
(1) (2)
(2)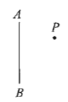
(3)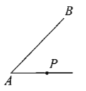 (4)
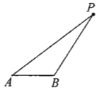
(4)
【答案】(1)见解析;(2)见解析;(3)见解析;(4)见解析
【解析】
(1)用三角板的一条直角边与AB重合,沿重合的直线平移三角板,使三角板的另一条直角边和P点重合,过P点沿直角边向AB画直线即可;
(2) 用三角板的一条直角边与AB重合,沿重合的直线平移三角板,使三角板的另一条直角边和P点重合,过P点沿直角边向AB画直线即可;
(3)用三角板的一条直角边与AB重合,沿重合的直线平移三角板,使三角板的另一条直角边和P点重合,过P点沿直角边向AB画直线即可;
(4)用三角板的一条直角边与AB重合,沿重合的直线平移三角板,使三角板的另一条直角边和P点重合,过P点沿直角边向AB画直线即可.
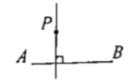
如图所示
(1)
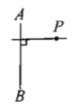
(2)
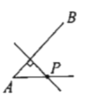
(3)
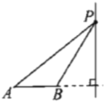
(4)


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】菱形![]() 中,
中,![]() ,
,![]() 是对角线,点
是对角线,点![]() 、
、![]() 分别是边
分别是边![]() 、
、![]() 上两个点,且满足
上两个点,且满足![]() ,连接
,连接![]() 与
与![]() 相交于点
相交于点![]() .
.
(1)如图1,求![]() 的度数;
的度数;
(2)如图2,作![]() 于
于![]() 点,求证:
点,求证:![]() ;
;
(3)在满足(2)的条件下,且点![]() 在菱形内部,若
在菱形内部,若![]() ,
,![]() ,求菱形
,求菱形![]() 的面积.
的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是一个边长为2的等边三角形,AD0⊥BC,垂足为点D0.过点D0作D0D1⊥AB,垂足为点D1;再过点D1作D1D2⊥AD0,垂足为点D2;又过点D2作D2D3⊥AB,垂足为点D3;……;这样一直作下去,得到一组线段:D0D1,D1D2,D2D3,……,则线段D1D2的长为______,线段Dn-1Dn的长为______(n为正整数).

查看答案和解析>>
科目:初中数学 来源: 题型:
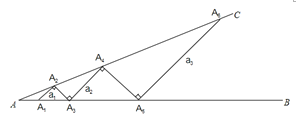
【题目】在∠A(0°<∠A<90°)的内部画线段,并使线段的两端点分别落在角的两边AB、AC上,如图所示,从点A1开始,依次向右画线段,使线段与线段在两端点处互相垂直,A1A2为第1条线段.设AA1=A1A2=A2A3=1,则∠A =_____![]() ;若记线段A2n-1A2n的长度为an(n为正整数),如A1A2=a1,A3A4=a2,则此时a2=_______,an=________(用含n的式子表示).
;若记线段A2n-1A2n的长度为an(n为正整数),如A1A2=a1,A3A4=a2,则此时a2=_______,an=________(用含n的式子表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算下列各题
(1)﹣2+(﹣7)+8.
(2)25﹣13﹣4﹣25.
(3)![]() .
.
(4)(﹣2.4)﹣(﹣4.5)+|﹣2.4|+(﹣0.5).
(5)(![]() )×(﹣36).
)×(﹣36).
(6)![]() .
.
(7)![]() ×(﹣12).
×(﹣12).
(8)13×(﹣![]() )+(﹣13)×
)+(﹣13)×![]() +13×
+13×![]() .
.
(9)﹣12018+![]() .
.
(10)![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有五张正面分别标有数字—2、—1、0、1、2的不透明卡片,它们除数字不同外其余全部相同,现将它们背面向上,洗匀后从中任取一张,将卡片上的数字记为![]() ,则
,则![]() 使关于
使关于![]() 的一元一次方程
的一元一次方程![]() 有整数解,且方程的整数解能与2,6组成三角形的概率是____________.
有整数解,且方程的整数解能与2,6组成三角形的概率是____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数轴上,我们把表示数2的点定为核点,记作点![]() ,对于两个不同的点
,对于两个不同的点![]() 和
和![]() ,若点
,若点![]() ,
,![]() 到点
到点![]() 的距离相等,则称点
的距离相等,则称点![]() 与点
与点![]() 互为核等距点.如图,点
互为核等距点.如图,点![]() 表示数-1,点
表示数-1,点![]() 表示数5,它们与核点
表示数5,它们与核点![]() 的距离都是3个单位长度,我们称点
的距离都是3个单位长度,我们称点![]() 与点
与点![]() 互为核等距点.
互为核等距点.
![]()
(1)已知点![]() 表示数3,如果点
表示数3,如果点![]() 与点
与点![]() 互为核等距点,那么点
互为核等距点,那么点![]() 表示的数是______;
表示的数是______;
(2)已知点![]() 表示数
表示数![]() ,点
,点![]() 与点
与点![]() 互为核等距点,
互为核等距点,
①如果点![]() 表示数
表示数![]() ,求
,求![]() 的值;
的值;
②对点![]() 进行如下操作:先把点
进行如下操作:先把点![]() 表示的数乘以2,再把所得数表示的点沿着数轴向左移动5个单位长度得到点
表示的数乘以2,再把所得数表示的点沿着数轴向左移动5个单位长度得到点![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
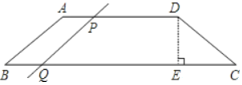
【题目】如图,在四边形ABCD中,AD∥BC,AB=CD,DE⊥BC于点E,且DE=![]() ,AD=18,∠C=60°;
,AD=18,∠C=60°;
(1)BC=________
(2)若动点P从点D出发,速度为2个单位/秒,沿DA向点A运动,同时,动点Q从点B出发,速度为3个单位/秒,沿BC向点C运动,当一个动点到达端点时,另一个动点同时停止运动,设运动的时间为t秒。
①t=_______秒时,四边形PQED是矩形;
②t为何值时,线段PQ与四边形ABCD的边构成平行四边形;
③是否存在t值,使②中的平行四边形是菱形?若存在,请求出t值,若不存在,请说明理由。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com