
【题目】菱形![]() 中,
中,![]() ,
,![]() 是对角线,点
是对角线,点![]() 、
、![]() 分别是边
分别是边![]() 、
、![]() 上两个点,且满足
上两个点,且满足![]() ,连接
,连接![]() 与
与![]() 相交于点
相交于点![]() .
.
(1)如图1,求![]() 的度数;
的度数;
(2)如图2,作![]() 于
于![]() 点,求证:
点,求证:![]() ;
;
(3)在满足(2)的条件下,且点![]() 在菱形内部,若
在菱形内部,若![]() ,
,![]() ,求菱形
,求菱形![]() 的面积.
的面积.

【答案】(1)![]() ;(2)证明见解析;(3)
;(2)证明见解析;(3)![]() .
.
【解析】
(1)只要证明△DAE≌△BDF,推出∠ADE=∠DBF,由∠EGB=∠GDB+∠GBD=∠GDB+∠ADE=60°,推出∠BGD=180°-∠BGE=120°;
(2)如图3中,延长GE到M,使得GM=GB,连接BD、CG.由△MBD≌△GBC,推出DM=GC,∠M=∠CGB=60°,由CH⊥BG,推出∠GCH=30°,推出CG=2GH,由CG=DM=DG+GM=DG+GB,即可证明2GH=DG+GB;
(3)解直角三角形求出BC即可解决问题.
(1)如图,

![]() 四边形
四边形![]() 是菱形,
是菱形,
![]() ,
,
![]() ,
,
![]() 是等边三角形,
是等边三角形,
![]() ,
,![]() ,
,
在![]() 和
和![]() 中,
中,
 ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
(2)如图,延长![]() 到
到![]() ,使得
,使得![]() ,连接
,连接![]() .
.
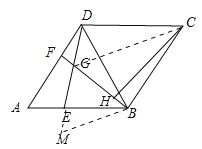
![]() ,
,![]() ,
,
![]() 是等边三角形,
是等边三角形,
![]() ,
,
![]() ,
,
在![]() 和
和![]() 中,
中,
 ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
(3)如图![]() 中,由(2)可知,在
中,由(2)可知,在![]() 中,
中,![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
在![]() 中,
中,![]() ,
,
![]() ,
,![]() 都是等边三角形,
都是等边三角形,
![]() .
.


 科学实验活动册系列答案
科学实验活动册系列答案科目:初中数学 来源: 题型:
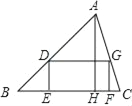
【题目】如图,△ABC是一块锐角三角形材料,高线AH长8cm,底边BC长10cm,要把它加工成一个矩形零件,使矩形DEFG的一边EF在BC上,其余两个顶点D、G分别在AB、AC上,AH交DG于M.
(1)求证:AMBC=AHDG;
(2)加工成的矩形零件DEFG的面积能否等于25cm2?若能,求出宽DE的长度;否则,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:a是单项式-xy2的系数,b是最小的正整数,c是多项式2m2n-m3n2-m-2的次数.请回答下列问题:
(1)请直接写出a、b、c的值.a= ,b= ,c= .
(2)数轴上,a、b、c三个数所对应的点分别为A、B、C,点A、B、C同时开始在数轴上运动,若点A以每秒1个单位长度的速度向左运动,同时,点B和点C分别以每秒1个单位长度和3个单位长度的速度向右运动,假设t秒钟过后,若点B与点c之间的距离表示为BC,点A与点C之间的距离表示为AC,点A与点C之间的距离表示为AC.
①t秒钟过后,AC的长度为 (用含t的关系式表示);
②请问:BC-AB的值是否会随着时间t的变化而改变?若变化,请说明理由;若不变,请求出其值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)5![]() -3
-3![]() +4
+4![]() -
-![]()
(2)(![]() -
-![]() -
-![]() )×(-36)
)×(-36)
(3)-![]() ―(1―0.5)÷
―(1―0.5)÷![]() ×[2+(-4)2]
×[2+(-4)2]
(4)(![]() -
-![]() )×52÷|-
)×52÷|-![]() |+(
|+(![]() )2019×42020
)2019×42020
查看答案和解析>>
科目:初中数学 来源: 题型:
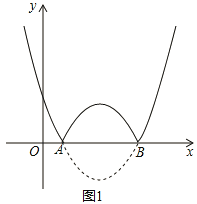
【题目】如图,抛物线![]() :
:![]() 与x轴交于A,B两点(点A在点B的左侧),将抛物线l在x轴下方部分沿x轴翻折,x轴上方的图像保持不变,就组成了函数
与x轴交于A,B两点(点A在点B的左侧),将抛物线l在x轴下方部分沿x轴翻折,x轴上方的图像保持不变,就组成了函数![]() 的图像.
的图像.
(1)若点A的坐标为(1,0).
①求抛物线![]() 的表达式,并直接写出当x为何值时,函数
的表达式,并直接写出当x为何值时,函数![]() 的值y随x的增大而增大;
的值y随x的增大而增大;
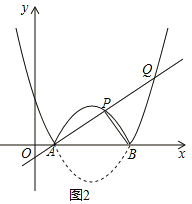
②如图2,若过A点的直线交函数![]() 的图像于另外两点P,Q,且
的图像于另外两点P,Q,且![]() ,求点P的坐标;
,求点P的坐标;
(2)当![]() 时,若函数
时,若函数![]() 的值y随x的增大而增大,直接写出h的取值范围.
的值y随x的增大而增大,直接写出h的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对任意一个正整数m,如果m=k(k+1),其中k是正整数,则称m为“矩数”,k 为m的最佳拆分点.例如,56=7×(7+1),则56是一个“矩数”,7为56的最佳拆分点.
(1)求证:若“矩数”m是3的倍数,则m一定是6的倍数;
(2)把“矩数”p与“矩数”q的差记为 D(p,q),其中p>q,D(p,q)>0.例如,20=4×5,6=2×3,则 D(20,6)=20﹣6=14.若“矩数”p的最佳拆分点为t,“矩数”q的最佳拆分点为s,当 D(p,q)=30时,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在学习了有理数的加减法之后,老师讲解了例题![]() 的计算思路为:将两个加数组合在一起作为一组,其和为1,共有1010组,所以结果为+1010.
的计算思路为:将两个加数组合在一起作为一组,其和为1,共有1010组,所以结果为+1010.
根据这个思路学生改编了下列几题:
(1)计算:①![]()
②![]()
(2)蚂蚁在数轴的原点![]() 处,第一次向右爬行1个单位,第二次向右爬行2个单位,第三次向左爬行3个单位,第四次向左爬行4个单位,第五次向右爬行5个单位,第六次向右爬行6个单位,第七次向左爬行7个单位……
处,第一次向右爬行1个单位,第二次向右爬行2个单位,第三次向左爬行3个单位,第四次向左爬行4个单位,第五次向右爬行5个单位,第六次向右爬行6个单位,第七次向左爬行7个单位……
①按照这个规律,第1024次爬行后蚂蚁所在位置在原点左侧还是右侧?对应哪个数?
②按照这个规律,第 次爬行后蚂蚁在数轴上表示751的位置.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点![]() (n为正整数)都在数轴上,点
(n为正整数)都在数轴上,点![]() 在原点O的左边,且
在原点O的左边,且![]() ;点
;点![]() 在原点O的右边,且
在原点O的右边,且![]() ;点
;点![]() 在原点O的左边,且
在原点O的左边,且![]() ;点
;点![]() 在 原点O的右边,且
在 原点O的右边,且![]() ;….依照上述规律,点
;….依照上述规律,点![]() ,
,![]() 所表示的数分别为( )
所表示的数分别为( )
A.1008,-1008B.1008,-1009
C.2016,-2017D.-2016,2017
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com