
ЁОЬтФПЁПШчЭМЃЌХзЮяЯп![]() ЃК
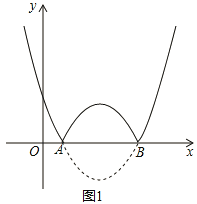
ЃК![]() гыxжсНЛгкAЃЌBСНЕуЃЈЕуAдкЕуBЕФзѓВрЃЉЃЌНЋХзЮяЯпlдкxжсЯТЗНВПЗжбиxжсЗелЃЌxжсЩЯЗНЕФЭМЯёБЃГжВЛБфЃЌОЭзщГЩСЫКЏЪ§
гыxжсНЛгкAЃЌBСНЕуЃЈЕуAдкЕуBЕФзѓВрЃЉЃЌНЋХзЮяЯпlдкxжсЯТЗНВПЗжбиxжсЗелЃЌxжсЩЯЗНЕФЭМЯёБЃГжВЛБфЃЌОЭзщГЩСЫКЏЪ§![]() ЕФЭМЯёЃЎ
ЕФЭМЯёЃЎ
ЃЈ1ЃЉШєЕуAЕФзјБъЮЊЃЈ1ЃЌ0ЃЉЃЎ
ЂйЧѓХзЮяЯп![]() ЕФБэДяЪНЃЌВЂжБНгаДГіЕБxЮЊКЮжЕЪБЃЌКЏЪ§
ЕФБэДяЪНЃЌВЂжБНгаДГіЕБxЮЊКЮжЕЪБЃЌКЏЪ§![]() ЕФжЕyЫцxЕФдіДѓЖјдіДѓЃЛ
ЕФжЕyЫцxЕФдіДѓЖјдіДѓЃЛ
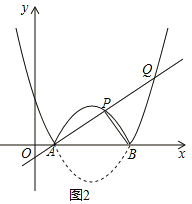
ЂкШчЭМ2ЃЌШєЙ§AЕуЕФжБЯпНЛКЏЪ§![]() ЕФЭМЯёгкСэЭтСНЕуPЃЌQЃЌЧв
ЕФЭМЯёгкСэЭтСНЕуPЃЌQЃЌЧв![]() ЃЌЧѓЕуPЕФзјБъЃЛ
ЃЌЧѓЕуPЕФзјБъЃЛ
ЃЈ2ЃЉЕБ![]() ЪБЃЌШєКЏЪ§
ЪБЃЌШєКЏЪ§![]() ЕФжЕyЫцxЕФдіДѓЖјдіДѓЃЌжБНгаДГіhЕФШЁжЕЗЖЮЇЃЎ
ЕФжЕyЫцxЕФдіДѓЖјдіДѓЃЌжБНгаДГіhЕФШЁжЕЗЖЮЇЃЎ
ЁОД№АИЁПЃЈ1ЃЉЂйЕБ![]() Лђ
Лђ![]() ЪБЃЌКЏЪ§
ЪБЃЌКЏЪ§![]() ЕФжЕyЫцxЕФдіДѓЖјдіДѓЃЌЂк PЕузјБъЮЊ
ЕФжЕyЫцxЕФдіДѓЖјдіДѓЃЌЂк PЕузјБъЮЊ![]() ЃЌ
ЃЌ![]() ЃЛЃЈ2ЃЉЕБ
ЃЛЃЈ2ЃЉЕБ![]() Лђ
Лђ![]() ЪБЃЌКЏЪ§
ЪБЃЌКЏЪ§![]() ЕФжЕyЫцxЕФдіДѓЖјдіДѓЃЎ
ЕФжЕyЫцxЕФдіДѓЖјдіДѓЃЎ
ЁОНтЮіЁПЗжЮіЃКЃЈ1ЃЉЂйРћгУД§ЖЈЯЕЪ§ЗЈЧѓХзЮяЯпЕФНтЮіЪНЃЌгЩЖдГЦадЧѓЕуBЕФзјБъЃЌИљОнЭМЯѓаДГіКЏЪ§ЕФжЕyЫцxЕФдіДѓЖјдіДѓЃЈМДГЪЩЯЩ§ЧїЪЦЃЉЕФxЕФШЁжЕЃЛ
ЂкШчЭМ2ЃЌзїИЈжњЯпЃЌЙЙНЈЖдГЦЕуFКЭжБНЧНЧШ§НЧаЮAQEЃЌИљОнSЁїABQ=2SЁїABPЃЌЕУQE=2PDЃЌжЄУїЁїPADЁзЁїQAEЃЌдђ![]() ЃЌЕУAE=2ADЃЌЩшAD=aЃЌИљОнQE=2FDСаЗНГЬПЩЧѓЕУaЕФжЕЃЌВЂМЦЫуPЕФзјБъЃЛ
ЃЌЕУAE=2ADЃЌЩшAD=aЃЌИљОнQE=2FDСаЗНГЬПЩЧѓЕУaЕФжЕЃЌВЂМЦЫуPЕФзјБъЃЛ
ЃЈ2ЃЉЯШСюy=0ЧѓХзЮяЯпгыxжсЕФСНИіНЛЕузјБъЃЌИљОнЭМЯѓжаГЪЩЯЩ§ЧїЪЦЕФВПЗжЃЌгаСНВПЗжЃКЗжБ№ЬжТлЃЌВЂСаВЛЕШЪНЛђВЛЕШЪНзщПЩЕУhЕФШЁжЕЃЎ
ЯъНтЃКЃЈ1ЃЉЂйЁпЕуAЃЈ1ЃЌ0ЃЉдкХзЮяЯп![]() ЩЯЃЌ
ЩЯЃЌ
Ёр ![]() ЃЎ
ЃЎ
НтЕУh=3Лђ![]() ЃЎ
ЃЎ
ЁпЕуAдкЕуBзѓВрЃЌ
Ёр![]() ЃЈЩсШЅЃЉЃЎ
ЃЈЩсШЅЃЉЃЎ
Ёр![]() ЃЎ
ЃЎ
Ёр ХзЮяЯпЕФБэДяЪНЮЊ![]() ЃЎ
ЃЎ
ЁрХзЮяЯпЕФЖдГЦжсЮЊжБЯп![]() ЃЎ
ЃЎ
ЁргЩЖдГЦадЕУBЃЈ5ЃЌ0ЃЉЃЎ
гЩЭМЯѓПЩжЊЃКЕБ![]() Лђ
Лђ![]() ЪБЃЌКЏЪ§
ЪБЃЌКЏЪ§![]() ЕФжЕyЫцxЕФдіДѓЖјдіДѓЃЎ
ЕФжЕyЫцxЕФдіДѓЖјдіДѓЃЎ
ЂкШчЭМ2ЃЌзїPDЁЭxжсгкЕуDЃЌбгГЄPDНЛХзЮяЯпlгкЕуFЃЌзїQEЁЭxжсгкЕуEЃЎ
гЩЖдГЦадПЩЕУ DF=PDЃЎ
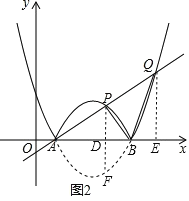
Ёп![]() ЃЌ
ЃЌ
Ёр![]() ЃЎ
ЃЎ
ЁрQE=2PDЃЎ
ЁпЁЯADP=ЁЯAEQ=90ЁуЃЌЁЯPAD=ЁЯEAQЃЎ
ЁрЁїPADЁзЁїQAEЃЎ
Ёр![]() ЃЎ
ЃЎ
ЁрAE=2ADЃЎ
ЩшAD=aЃЌдђOD=1+aЃЌOE=1+2aЃЌPЃЈ1+![]() ЃЌ
ЃЌ![]() ЃЉЃЎ
ЃЉЃЎ
ЁпЕуFЃЌQдкХзЮяЯп![]() ЩЯЃЌ
ЩЯЃЌ
Ёр![]() ЃЎ
ЃЎ
![]() ЃЎ
ЃЎ
Ёр![]() ЃЎ
ЃЎ
НтЕУЃК![]() Лђ
Лђ![]() ЃЈЩсШЅЃЉЃЎ
ЃЈЩсШЅЃЉЃЎ
ЁрPЕузјБъЮЊ![]() ЃЌ
ЃЌ![]() ЃЎ
ЃЎ
ЃЈ2ЃЉЃЈ2ЃЉЕБy=0ЪБЃЌ![]() ЃЈx-hЃЉ2-2=0ЃЌ
ЃЈx-hЃЉ2-2=0ЃЌ
НтЕУЃКx=h+2Лђx=h-2ЃЌ
ЁпЕуAдкЕуBЕФзѓВрЃЌЧвh>0ЃЌ
ЁрAЃЈh-2ЃЌ0ЃЉЃЌBЃЈh+2ЃЌ0ЃЉЃЌ
ШчЭМ3ЃЌзїХзЮяЯпЕФЖдГЦжсНЛХзЮяЯпгкЕуCЃЌ
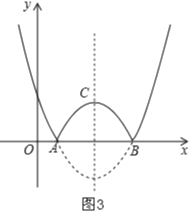
ЗжСНжжЧщПіЃК
ЂйгЩЭМЯѓПЩжЊЃКЭМЯѓfдкACЖЮЪБЃЌКЏЪ§fЕФжЕЫцxЕФдіДѓЖјдіДѓЃЌ
дђ![]() ЃЌ
ЃЌ
Ёр3ЁмhЁм4ЃЌ
ЂкгЩЭМЯѓПЩжЊЃКЭМЯѓfЕуBЕФгвВрЪБЃЌКЏЪ§fЕФжЕЫцxЕФдіДѓЖјдіДѓЃЌ
МДЃКh+2Ём2ЃЌ
hЁм0ЃЌ
злЩЯЫљЪіЃЌЕБ3ЁмhЁм4ЛђhЁм0ЪБЃЌКЏЪ§fЕФжЕЫцxЕФдіДѓЖјдіДѓЃЎ


 аЁбЇЖсЙкABОэЯЕСаД№АИ
аЁбЇЖсЙкABОэЯЕСаД№АИ ABCПМЭѕШЋгХОэЯЕСаД№АИ
ABCПМЭѕШЋгХОэЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЃЌе§ЗНаЮABCDжаЃЌ![]() ЃЌ
ЃЌ![]() ШЦЕуAЫГЪБеыа§зЊЃЌЫќЕФСНБпГЄЗжБ№НЛCBЁЂDCЛђЫќУЧЕФбгГЄЯп
ШЦЕуAЫГЪБеыа§зЊЃЌЫќЕФСНБпГЄЗжБ№НЛCBЁЂDCЛђЫќУЧЕФбгГЄЯп![]() гкЕуMNЃЌ
гкЕуMNЃЌ![]() гкЕуHЃЎ
гкЕуHЃЎ
![]() ШчЭМ
ШчЭМ![]() ЃЌЕБ
ЃЌЕБ![]() ЕуAа§зЊЕН
ЕуAа§зЊЕН![]() ЪБЃЌЧыФужБНгаДГіAHгыABЕФЪ§СПЙиЯЕЃЛ
ЪБЃЌЧыФужБНгаДГіAHгыABЕФЪ§СПЙиЯЕЃЛ
![]() ШчЭМ
ШчЭМ![]() ЃЌЕБ
ЃЌЕБ![]() ШЦЕуAа§зЊЕН
ШЦЕуAа§зЊЕН![]() ЪБЃЌ
ЪБЃЌ![]() жаЗЂЯжЕФAHгыABЕФЪ§СПЙиЯЕЛЙГЩСЂТ№ЃПШчЙћВЛГЩСЂЧыаДГіРэгЩЃЌШчЙћГЩСЂЧыжЄУїЃЎ
жаЗЂЯжЕФAHгыABЕФЪ§СПЙиЯЕЛЙГЩСЂТ№ЃПШчЙћВЛГЩСЂЧыаДГіРэгЩЃЌШчЙћГЩСЂЧыжЄУїЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
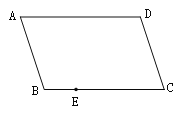
ЁОЬтФПЁПШчЭМЃЌЫФБпаЮABCDЪЧЦНааЫФБпаЮЃЌEЪЧBCБпЩЯвЛЕуЃЌжЛгУвЛАбЮоПЬЖШЕФжБГпдкADБпЩЯзїЕуFЃЌЪЙЕУDF=BE.
ЃЈ1ЃЉзїГіТњзуЬтвтЕФЕуFЃЌМђвЊЫЕУїФуЕФзїЭМЙ§ГЬЃЛ
ЃЈ2ЃЉвРОнФуЕФзїЭМЃЌжЄУїЃКDF=BE.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
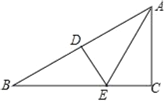
ЁОЬтФПЁПШчЭМЃЌдкЁїABCжаЃЌЁЯBЃН30ЁуЃЌБпABЕФДЙжБЦНЗжЯпЗжБ№НЛABКЭBCгкЕуDЃЌEЃЌЧвAEЦНЗжЁЯBACЃЎ
ЃЈ1ЃЉЧѓЁЯCЕФЖШЪ§ЃЛ
ЃЈ2ЃЉШєCEЃН1ЃЌЧѓABЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЁОдФЖСРэНтЁПЖдгкШЮвте§ЪЕЪ§aЁЂbЃЌвђЮЊ![]() Ён0ЃЌЫљвд
Ён0ЃЌЫљвд![]()
![]() Ён0ЃЌЫљвд
Ён0ЃЌЫљвд![]() Ён2
Ён2![]() ЃЌжЛгаЕБ
ЃЌжЛгаЕБ![]() ЪБЃЌЕШКХГЩСЂЃЎ
ЪБЃЌЕШКХГЩСЂЃЎ
ЁОЛёЕУНсТлЁПдк![]() Ён2
Ён2![]() ЃЈaЁЂbОљЮЊе§ЪЕЪ§ЃЉжаЃЌШє
ЃЈaЁЂbОљЮЊе§ЪЕЪ§ЃЉжаЃЌШє![]() ЮЊЖЈжЕ
ЮЊЖЈжЕ![]() ЃЌдђ
ЃЌдђ![]() Ён2
Ён2![]() ЃЌжЛгаЕБ
ЃЌжЛгаЕБ![]() ЪБЃЌ
ЪБЃЌ ![]() газюаЁжЕ2
газюаЁжЕ2![]() ЃЎ
ЃЎ
ИљОнЩЯЪіФкШнЃЌЛиД№ЯТСаЮЪЬтЃКШє![]() >0ЃЌжЛгаЕБ
>0ЃЌжЛгаЕБ![]() = ЪБЃЌ
= ЪБЃЌ ![]() газюаЁжЕ ЃЎ
газюаЁжЕ ЃЎ
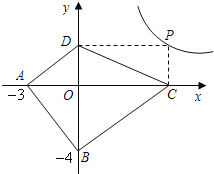
ЁОЬНЫїгІгУЁПШчЭМЃЌвбжЊAЃЈЃ3ЃЌ0ЃЉЃЌBЃЈ0ЃЌЃ4ЃЉЃЌPЮЊЫЋЧњЯп![]() ЃЈ
ЃЈ![]() ЃО0ЃЉЩЯЕФШЮвтвЛЕуЃЌЙ§ЕуPзїPCЁЭxжсгкЕуCЃЌPDЁЭyжсгкЕуDЃЎЧѓЫФБпаЮABCDУцЛ§ЕФзюаЁжЕЃЌВЂЫЕУїДЫЪБЫФБпаЮABCDЕФаЮзДЃЎ
ЃО0ЃЉЩЯЕФШЮвтвЛЕуЃЌЙ§ЕуPзїPCЁЭxжсгкЕуCЃЌPDЁЭyжсгкЕуDЃЎЧѓЫФБпаЮABCDУцЛ§ЕФзюаЁжЕЃЌВЂЫЕУїДЫЪБЫФБпаЮABCDЕФаЮзДЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПСтаЮ![]() жаЃЌ
жаЃЌ![]() ЃЌ
ЃЌ![]() ЪЧЖдНЧЯпЃЌЕу
ЪЧЖдНЧЯпЃЌЕу![]() ЁЂ
ЁЂ![]() ЗжБ№ЪЧБп
ЗжБ№ЪЧБп![]() ЁЂ
ЁЂ![]() ЩЯСНИіЕуЃЌЧвТњзу
ЩЯСНИіЕуЃЌЧвТњзу![]() ЃЌСЌНг
ЃЌСЌНг![]() гы
гы![]() ЯрНЛгкЕу
ЯрНЛгкЕу![]() ЃЎ
ЃЎ
(1)ШчЭМ1ЃЌЧѓ![]() ЕФЖШЪ§ЃЛ
ЕФЖШЪ§ЃЛ
(2)ШчЭМ2ЃЌзї![]() гк
гк![]() ЕуЃЌЧѓжЄЃК
ЕуЃЌЧѓжЄЃК![]() ЃЛ
ЃЛ
(3)дкТњзу(2)ЕФЬѕМўЯТЃЌЧвЕу![]() дкСтаЮФкВПЃЌШє
дкСтаЮФкВПЃЌШє![]() ЃЌ
ЃЌ![]() ЃЌЧѓСтаЮ
ЃЌЧѓСтаЮ![]() ЕФУцЛ§ЃЎ
ЕФУцЛ§ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌНЋЫФеХБпГЄИїВЛЯрЭЌЕФе§ЗНаЮжНЦЌАДШчЭМЗНЪНЗХШыОиаЮABCDФкЃЈЯрСкжНЦЌжЎМфЛЅВЛжиЕўвВЮоЗьЯЖЃЉЃЌЮДБЛЫФеХе§ЗНаЮжНЦЌИВИЧЕФВПЗжгУвѕгАБэЪОЃЌЩшгвЩЯНЧгызѓЯТНЧвѕгАВПЗжЕФжмГЄЕФВюЮЊlЃЎШєжЊЕРlЕФжЕЃЌдђВЛашвЊВтСПОЭФмжЊЕРжмГЄЕФе§ЗНаЮЕФБъКХЮЊЃЈ ЃЉ

A.ЂйB.ЂкC.ЂлD.Ђм
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
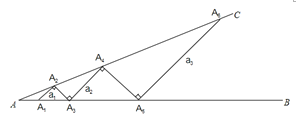
ЁОЬтФПЁПдкЁЯAЃЈ0ЁуЃМЁЯAЃМ90ЁуЃЉЕФФкВПЛЯпЖЮЃЌВЂЪЙЯпЖЮЕФСНЖЫЕуЗжБ№ТфдкНЧЕФСНБпABЁЂACЩЯЃЌШчЭМЫљЪОЃЌДгЕуA1ПЊЪМЃЌвРДЮЯђгвЛЯпЖЮЃЌЪЙЯпЖЮгыЯпЖЮдкСНЖЫЕуДІЛЅЯрДЙжБЃЌA1A2ЮЊЕк1ЬѕЯпЖЮ.ЩшAA1=A1A2=A2A3=1ЃЌдђЁЯA =_____![]() ЃЛШєМЧЯпЖЮA2n-1A2nЕФГЄЖШЮЊanЃЈnЮЊе§ећЪ§ЃЉЃЌШчA1A2=a1,A3A4=a2ЃЌдђДЫЪБa2=_______ЃЌan=________ЃЈгУКЌnЕФЪНзгБэЪОЃЉ.
ЃЛШєМЧЯпЖЮA2n-1A2nЕФГЄЖШЮЊanЃЈnЮЊе§ећЪ§ЃЉЃЌШчA1A2=a1,A3A4=a2ЃЌдђДЫЪБa2=_______ЃЌan=________ЃЈгУКЌnЕФЪНзгБэЪОЃЉ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдФЖСРэНтВЂНтД№ЃК
ЮЊСЫЧѓ1+2+22+23+24+Ё+22009ЕФжЕЃЌПЩСюSЃН1+2+22+23+24+Ё+22009ЃЌ
дђ2SЃН2+22+23+24+Ё+22009+22010ЃЌвђДЫ2SЉSЃНЃЈ2+22+23+Ё+22009+22010ЃЉЉЃЈ1+2+22+23+Ё+22009ЃЉЃН22010Љ1ЃЎ
ЫљвдЃКSЃН22010Љ1ЃЎМД1+2+22+23+24+Ё+22009ЃН22010Љ1ЃЎ
ЧывРееДЫЗЈЃЌЧѓЃК1+4+42+43+44+Ё+42010ЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com