
����Ŀ�����Ķ����⡿����������ʵ��a��b����Ϊ![]() ��0������
��0������![]()
![]() ��0������
��0������![]() ��2
��2![]() ��ֻ�е�
��ֻ�е�![]() ʱ���Ⱥų�����
ʱ���Ⱥų�����
����ý��ۡ���![]() ��2
��2![]() ��a��b��Ϊ��ʵ�����У���
��a��b��Ϊ��ʵ�����У���![]() Ϊ��ֵ
Ϊ��ֵ![]() ����
����![]() ��2
��2![]() ��ֻ�е�
��ֻ�е�![]() ʱ��
ʱ�� ![]() ����Сֵ2
����Сֵ2![]() ��
��
�����������ݣ��ش��������⣺��![]() >0��ֻ�е�
>0��ֻ�е�![]() = ʱ��
= ʱ�� ![]() ����Сֵ ��
����Сֵ ��
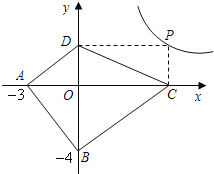
��̽��Ӧ�á���ͼ����֪A����3��0����B��0����4����PΪ˫����![]() ��
��![]() ��0���ϵ�����һ�㣬����P��PC��x���ڵ�C��PD��y���ڵ�D�����ı���ABCD�������Сֵ����˵����ʱ�ı���ABCD����״��
��0���ϵ�����һ�㣬����P��PC��x���ڵ�C��PD��y���ڵ�D�����ı���ABCD�������Сֵ����˵����ʱ�ı���ABCD����״��
���𰸡���1��1��2��2������
����������������1��������Ŀ������Ϣ��֪m+![]() ��2
��2![]() ���ҵ�m=
���ҵ�m=![]() ʱ�Ⱥų������ɵó�����
ʱ�Ⱥų������ɵó�����
��2������P��x�� ![]() �����ɱ�ʾ��AC��BD�����ı���ABCD�����ΪS�ı���ABCD=2��x+
�����ɱ�ʾ��AC��BD�����ı���ABCD�����ΪS�ı���ABCD=2��x+![]() ��+12��������������Ϣ�ɵõ�����Сֵ����ʱx=3���ɵó�AC=BD���ɵó��ı���ABCDΪ���Σ�
��+12��������������Ϣ�ɵõ�����Сֵ����ʱx=3���ɵó�AC=BD���ɵó��ı���ABCDΪ���Σ�
�������1��������Ŀ������Ϣ��֪m+![]() ��2
��2![]() ���ҵ�m=
���ҵ�m=![]() ʱ�Ⱥ����൱m=1ʱ��m+
ʱ�Ⱥ����൱m=1ʱ��m+![]() ��2������m=1ʱ��m+
��2������m=1ʱ��m+![]() ����Сֵ2���ʴ�Ϊ��1��2��
����Сֵ2���ʴ�Ϊ��1��2��
��2����P��x�� ![]() ������C��x��0����D��0��
������C��x��0����D��0�� ![]() ������CA=x+3��BD=
������CA=x+3��BD=![]() +4����S�ı���ABCD=
+4����S�ı���ABCD=![]() CA��BD=
CA��BD=![]() ��x+3����
��x+3����![]() +4�����������S=2��x+
+4�����������S=2��x+![]() ��+12����x��0��
��+12����x��0�� ![]() ��0����x+
��0����x+![]() ��2
��2![]() =6��ֻ�е�x=
=6��ֻ�е�x=![]() ����x=3ʱ���Ⱥų�������S��2��6+12=24�����ı���ABCD���������Сֵ24����ʱ��P��3��4����C��3��0����D��0��4����AB=BC=CD=DA=5�����ı���ABCD�����Σ�
����x=3ʱ���Ⱥų�������S��2��6+12=24�����ı���ABCD���������Сֵ24����ʱ��P��3��4����C��3��0����D��0��4����AB=BC=CD=DA=5�����ı���ABCD�����Σ�


 ʱ�����������ҵԭ���ܳ�����ϵ�д�
ʱ�����������ҵԭ���ܳ�����ϵ�д� ����νӽ̲���ĩ���Ԥϰ�人������ϵ�д�
����νӽ̲���ĩ���Ԥϰ�人������ϵ�д� ������ҵ��ٳɳ����½������������ϵ�д�
������ҵ��ٳɳ����½������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����x��һԪ���η���x2��x+a��1=0��
��1����a=��11ʱ����������̣�
��2�����������������ʵ����x1��x2����a��ȡֵ��Χ��
��3������������ʵ����x1��x2����[2+x1��1��x1��][2+x2��1��x2��]=9����a��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
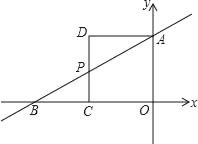
����Ŀ����ͼ����ֱ������ϵ�У�ֱ��AB�ֱ���x�ᡢy�ύ��B��A���㣬OA��OB�ij��ǹ���x��һԪ���η���x2��12x+32=0������ʵ��������OB��OA����OAΪһ������ͼ��ʾ��������AOCD��CD��AB�ڵ�P��
��1����ֱ��AB�Ľ���ʽ��
��2����x�����Ƿ����һ��Q��ʹ��P��C��QΪ���������������ADP���ƣ������ڣ����Q���ꣻ����˵�����ɣ�
��3����N��ƽ����һ���㣬��y�����Ƿ���ڵ�M��ʹ����A��C��M��NΪ������ı��������Σ������ڣ���ֱ��д����M�����ꣻ������˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
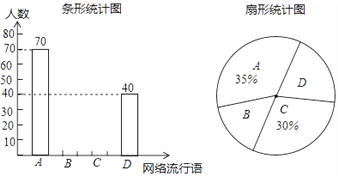
����Ŀ��������ʱ���ÿ�������϶�����ֺܶ�켫һʱ�����������Ϊ�˽�ͬѧ�Ƕ������������ʹ�������ij��ѧ��ȤС��ѡȡ�����е� A���������㹽����B�������֮������C������˾������D������·���ĸ�������������ȫУ3000��ѧ���н����˳������飬Ҫ��ÿλ������ѧ��ֻ�ܴ���ѡ��һ���Լ��õ�����������������ݵ���������С�����������������������ͳ��ͼ������ͼ���ṩ����Ϣ���벹ȫ����ͳ��ͼ�����Ƹ�Уѧ���õ��������������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������������ʵ���ԣ�a��b���ͣ�c��d�����涨�����ҽ���a��c��b��dʱ�� ��a��b������c��d��������������![]() ������a��b��
������a��b��![]() ��c��d������ac��bd��ad��bc��������1��2��
��c��d������ac��bd��ad��bc��������1��2��![]() ��p��3������q��q������pq��___________��
��p��3������q��q������pq��___________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
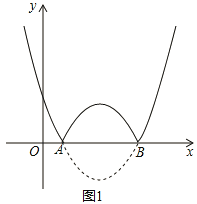
����Ŀ����ͼ��������![]() ��
��![]() ��x�ύ��A��B���㣨��A�ڵ�B����ࣩ����������l��x���·�������x�ᷭ�ۣ�x���Ϸ���ͼ�ֲ��䣬������˺���
��x�ύ��A��B���㣨��A�ڵ�B����ࣩ����������l��x���·�������x�ᷭ�ۣ�x���Ϸ���ͼ�ֲ��䣬������˺���![]() ��ͼ��
��ͼ��
��1������A��������1��0����
����������![]() �ı���ʽ����ֱ��д����xΪ��ֵʱ������
�ı���ʽ����ֱ��д����xΪ��ֵʱ������![]() ��ֵy��x�����������
��ֵy��x�����������
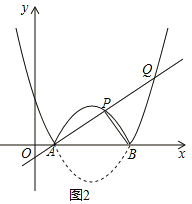
����ͼ2������A���ֱ�߽�����![]() ��ͼ������������P��Q����
��ͼ������������P��Q����![]() �����P�����ꣻ
�����P�����ꣻ
��2����![]() ʱ��������
ʱ��������![]() ��ֵy��x�����������ֱ��д��h��ȡֵ��Χ��
��ֵy��x�����������ֱ��д��h��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
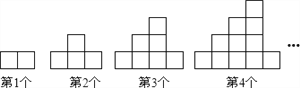
����Ŀ����ͼ������ͼ�������ɳ�����ͬ�Ļ��һ���Ĺ���ƴ����ɣ�Χ�ɵ�ÿ��С���������Ϊ1![]() .��һ��ͼ�����Ϊ2
.��һ��ͼ�����Ϊ2![]() ���ڶ���ͼ�����Ϊ4
���ڶ���ͼ�����Ϊ4![]() ��������ͼ�����Ϊ7
��������ͼ�����Ϊ7![]() �������˹��ɣ���8��ͼ�����Ϊ�� ��
�������˹��ɣ���8��ͼ�����Ϊ�� ��
A. 34![]() B. 35
B. 35 ![]() C. 36
C. 36![]() D. 37
D. 37![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijͬѧҪ֤��������ƽ���ı��εĶԱ���ȣ�������ȷ�ģ���������ͼ�Σ���д����������֪�Ͳ���������֤��
��֪����ͼ���ı���ABCD��ƽ���ı��Σ�
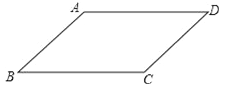
��֤��AB=CD��
��1����ȫ��֤���֣�
��2������д��֤�����̣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ��ͯ��A����������ͯ����B����A��B��Ӱ��ľ���AC��BD�ij��ֱ�Ϊ500��700�ף���C��D���صľ���Ϊ1600�ף����ǰ��ͯ��A�㽫��ǣ�����ӱ�ȥ��ˮ���ٸϻؼң���ô��ͯ����Ҫ�ߵľ����ǣ� ��
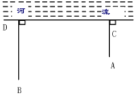
A. 2600��B. 2300��C. 2000��D. 1200��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com