
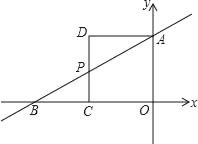
°æƒø°ø»ÁÕº£¨‘⁄÷±Ω«◊¯±Íœµ÷–£¨÷±œþAB∑÷±”Îx÷·°¢y÷·Ωª”⁄B°¢A¡Ωµ„£¨OA°¢OBµƒ≥§ «πÿ”⁄xµƒ“ª‘™∂˛¥Œ∑Ω≥Ãx2©Å12x+32=0µƒ¡Ω∏ˆ µ ˝∏˘£¨«“OB£æOA£¨“‘OAŒ™“ª±þ◊˜»ÁÕºÀ˘ 浃’˝∑Ω–ŒAOCD£¨CDΩªAB”⁄µ„P£Æ
£®1£©«Û÷±œþABµƒΩ‚Œˆ Ω£ª
£®2£©‘⁄x÷·…œ «∑ҥʑ⁄“ªµ„Q£¨ π“‘P°¢C°¢QŒ™∂•µ„µƒ»˝Ω«–Œ”ΰ˜ADPœýÀ∆£ø»Ù¥Ê‘⁄£¨«Ûµ„Q◊¯±Í£ª∑Ò‘Ú£¨Àµ√˜¿Ì”…£ª
£®3£©…ËN «∆Ω√ʃ⁄“ª∂ص„£¨‘⁄y÷·…œ «∑ҥʑ⁄µ„M£¨ πµ√“‘A°¢C°¢M°¢NŒ™∂•µ„µƒÀƒ±þ–Œ «¡‚–Œ£ø»Ù¥Ê‘⁄£¨«Î÷±Ω”–¥≥ˆµ„Mµƒ◊¯±Í£ª∑Ò‘Ú£¨«ÎÀµ√˜¿Ì”…£Æ
°æ¥∞∏°ø£®1£©y=![]() x+4£ª£®2£©¥Ê‘⁄¬˙◊„Ãıº˛µƒµ„Q£¨∆‰◊¯±ÍŒ™£®©Å8£¨0£©ªÚ£®0£¨0£©ªÚ£®©Å3£¨0£©ªÚ£®©Å5£¨0£©£ª£®3£©¥Ê‘⁄¬˙◊„Ãıº˛µƒMµ„£¨∆‰◊¯±ÍŒ™£®0£¨4+4
x+4£ª£®2£©¥Ê‘⁄¬˙◊„Ãıº˛µƒµ„Q£¨∆‰◊¯±ÍŒ™£®©Å8£¨0£©ªÚ£®0£¨0£©ªÚ£®©Å3£¨0£©ªÚ£®©Å5£¨0£©£ª£®3£©¥Ê‘⁄¬˙◊„Ãıº˛µƒMµ„£¨∆‰◊¯±ÍŒ™£®0£¨4+4![]() £©ªÚ£®0£¨4©Å4
£©ªÚ£®0£¨4©Å4![]() £©ªÚ£®0£¨0£©£Æ
£©ªÚ£®0£¨0£©£Æ
°æΩ‚Œˆ°ø ‘Â∑÷Œˆ£∫£®1£©”…∑Ω≥Ãø…«Ûµ√OA°¢OBµƒ≥§£¨‘Úø…«Ûµ√![]() µƒ◊¯±Í£¨¿˚”√¥˝∂®œµ ˝∑®ø…«Ûµ√÷±œþ
µƒ◊¯±Í£¨¿˚”√¥˝∂®œµ ˝∑®ø…«Ûµ√÷±œþ![]() µƒΩ‚Œˆ Ω£ª
µƒΩ‚Œˆ Ω£ª
£®2£©…ËQ(x,0)£¨‘ÚCQ=|x+4|£¨∑÷![]() ∫Õ
∫Õ![]() ¡Ω÷÷«Èøˆ£¨¿˚”√œýÀ∆»˝Ω«–Œµƒ–‘÷ ø…∑÷±µ√µΩπÿ”⁄
¡Ω÷÷«Èøˆ£¨¿˚”√œýÀ∆»˝Ω«–Œµƒ–‘÷ ø…∑÷±µ√µΩπÿ”⁄![]() µƒ∑Ω≥㨑Úø…«Ûµ√
µƒ∑Ω≥㨑Úø…«Ûµ√![]() µƒ÷µ£¨ø…«Ûµ√
µƒ÷µ£¨ø…«Ûµ√![]() µ„◊¯±Í£ª
µ„◊¯±Í£ª
£®3£©µ±![]() Œ™¡‚–Œµƒ±þ ±£¨‘Ú”–
Œ™¡‚–Œµƒ±þ ±£¨‘Ú”–![]() ø…«Ûµ√
ø…«Ûµ√![]() µ„◊¯±Í£ªµ±
µ„◊¯±Í£ªµ±![]() Œ™∂‘Ω«œþ ±£¨”…Õº–Œø…÷™
Œ™∂‘Ω«œþ ±£¨”…Õº–Œø…÷™![]() µ„º¥Œ™À˘«Û£¨ø…«Ûµ√
µ„º¥Œ™À˘«Û£¨ø…«Ûµ√![]() µ„◊¯±Í£Æ
µ„◊¯±Í£Æ
‘Ã‚Ω‚Œˆ£∫(1)Ω‚∑Ω≥Ã![]() ø…µ√x=4ªÚx=8£¨
ø…µ√x=4ªÚx=8£¨
°þOA°¢OBµƒ≥§ «πÿ”⁄xµƒ“ª‘™∂˛¥Œ∑Ω≥Ã![]() µƒ¡Ω∏ˆ µ ˝∏˘£¨«“OB>OA£¨
µƒ¡Ω∏ˆ µ ˝∏˘£¨«“OB>OA£¨
°ýOA=4£¨OB=8£¨
°ýA(0,4),B(8,0)£¨
…Ë÷±œþABΩ‚Œˆ ΩŒ™y=kx+b£¨
°ý![]() Ω‚µ√
Ω‚µ√
°ý÷±œþABΩ‚Œˆ ΩŒ™![]()
(2)°þÀƒ±þ–ŒAOCDŒ™’˝∑Ω–Œ£¨
°ýAD=CD=OC=OA=4£¨
°ýC(4,0)£¨
‘⁄![]() ÷–£¨¡Óx=4£¨ø…µ√y=2£¨
÷–£¨¡Óx=4£¨ø…µ√y=2£¨
°ýPC=PD=2£¨
…ËQ(x,0)£¨‘ÚCQ=|x+4|£¨
°þ“‘P°¢C.QŒ™∂•µ„µƒ»˝Ω«–Œ”ΰ˜ADPœýÀ∆£¨
°ý”–°˜PCQ°◊°˜PDA∫Õ°˜PCQ°◊°˜ADP¡Ω÷÷«Èøˆ£¨
¢Ÿµ±°˜PCQ°◊°˜PDA ±,‘Ú”–![]() ,º¥
,º¥![]() ,Ω‚µ√x=0ªÚx=8,¥À ±Qµ„◊¯±ÍŒ™(8,0)ªÚ(0,0)£ª
,Ω‚µ√x=0ªÚx=8,¥À ±Qµ„◊¯±ÍŒ™(8,0)ªÚ(0,0)£ª
¢⁄µ±°˜PCQ°◊°˜ADP ±,‘Ú”–![]() º¥
º¥![]() ,Ω‚µ√x=3ªÚx=5,¥À ±Qµ„◊¯±ÍŒ™(3,0)ªÚ(5,0)£ª
,Ω‚µ√x=3ªÚx=5,¥À ±Qµ„◊¯±ÍŒ™(3,0)ªÚ(5,0)£ª
◊€…œø…÷™¥Ê‘⁄¬˙◊„Ãıº˛µƒµ„Q,∆‰◊¯±ÍŒ™(8,0)ªÚ(0,0)ªÚ(3,0)ªÚ(5,0)£ª
(3)”…“‚ø……ËM(0,y)£¨
°þA(0,4),C(4,0)£¨
°ý![]()
µ±ACŒ™¡‚–Œµƒ“ª±þ ±,‘Ú”–AC=AM,º¥|y4|=![]() ,Ω‚µ√y=4°¿
,Ω‚µ√y=4°¿![]() ,¥À ±Mµ„◊¯±ÍŒ™
,¥À ±Mµ„◊¯±ÍŒ™![]() ªÚ
ªÚ![]()
µ±ACŒ™¡‚–Œµƒ∂‘Ω«œþ ±,‘Ú”–MA=MC,”…“‚ø…÷™¥À ±Mµ„º¥Œ™Oµ„,¥À ±Mµ„◊¯±ÍŒ™(0,0)£ª
◊€…œø…÷™¥Ê‘⁄¬˙◊„Ãıº˛µƒMµ„,∆‰◊¯±ÍŒ™![]() ªÚ
ªÚ![]() ªÚ(0,0).
ªÚ(0,0).


 –¬ÀºŒ¨ºŸ∆⁄◊˜“µ ÓºŸº™¡÷¥Û—ß≥ˆ∞Ê…Áœµ¡–¥∞∏
–¬ÀºŒ¨ºŸ∆⁄◊˜“µ ÓºŸº™¡÷¥Û—ß≥ˆ∞Ê…Áœµ¡–¥∞∏ ¿∂ÃÏΩÔ˝ ÓºŸ”≈ªØ—ßœ∞œµ¡–¥∞∏
¿∂ÃÏΩÔ˝ ÓºŸ”≈ªØ—ßœ∞œµ¡–¥∞∏
| ƒÍº∂ | ∏þ÷–øŒ≥à | ƒÍº∂ | ≥ı÷–øŒ≥à |
| ∏þ“ª | ∏þ“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı“ª | ≥ı“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ∂˛ | ∏þ∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı∂˛ | ≥ı∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ»˝ | ∏þ»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı»˝ | ≥ı»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° |
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
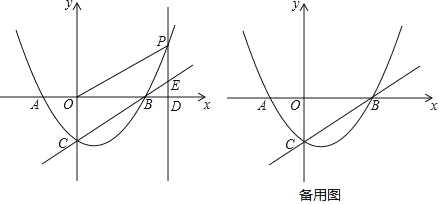
°æƒø°ø»ÁÕº£¨≈◊ŒÔœþy=ax2+bx©Å2µƒ∂‘≥∆÷· «÷±œþx=1£¨”Îx÷·Ωª”⁄A£¨B¡Ωµ„£¨”Îy÷·Ωª”⁄µ„C£¨µ„Aµƒ◊¯±ÍŒ™£®©Å2£¨0£©£¨µ„PŒ™≈◊ŒÔœþ…œµƒ“ª∏ˆ∂ص„£¨π˝µ„P◊˜PD°Õx÷·”⁄µ„D£¨Ωª÷±œþBC”⁄µ„E£Æ
£®1£©«Û≈◊ŒÔœþΩ‚Œˆ Ω£ª
£®2£©»Ùµ„P‘⁄µ⁄“ªœÛœÞƒ⁄£¨µ±OD=4PE ±£¨«ÛÀƒ±þ–ŒPOBEµƒ√ʪ˝£ª
£®3£©‘⁄£®2£©µƒÃıº˛œ¬£¨»Ùµ„MŒ™÷±œþBC…œ“ªµ„£¨µ„NŒ™∆Ω√Ê÷±Ω«◊¯±Íœµƒ⁄“ªµ„£¨ «∑ҥʑ⁄’‚—˘µƒµ„M∫Õµ„N£¨ πµ√“‘µ„B£¨D£¨M£¨NŒ™∂•µ„µƒÀƒ±þ–Œ «¡‚–Œ£ø»Ù¥Ê‘⁄£¨÷±Ω”–¥≥ˆµ„Nµƒ◊¯±Í£ª»Ù≤ª¥Ê‘⁄£¨«ÎÀµ√˜¿Ì”…£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øŒ“ –ƒ≥¥¢‘À≤øΩÙº±µ˜≤¶“ª≈˙ŒÔ◊ £¨µ˜Ω¯ŒÔ◊ π≤”√4–° ±£¨µ˜Ω¯ŒÔ◊ 2–° ±∫Ûø™ ºµ˜≥ˆŒÔ◊ £®µ˜Ω¯ŒÔ◊ ”ε˜≥ˆŒÔ◊ µƒÀŸ∂»æ˘±£≥÷≤ª±‰£©£Æ¥¢‘À≤øø‚¥ÊŒÔ◊ S£®∂÷£©”Î ±º‰t£®–° ±£©÷ƺ‰µƒ∫Ø ˝πÿœµ»ÁÕºÀ˘ 棨’‚≈˙ŒÔ◊ ¥”ø™ ºµ˜Ω¯µΩ»´≤øµ˜≥ˆ–Ë“™µƒ ±º‰ «_________–° ±.

≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
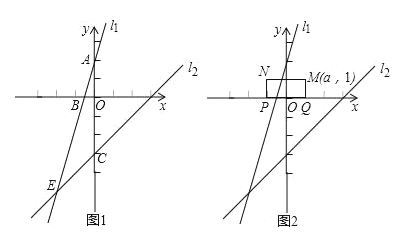
°æƒø°ø»ÁÕº1£¨‘⁄÷±Ω«◊¯±Íœµ÷–£¨“ª¥Œ∫Ø ˝µƒÕºœÛl![]() ”Îy÷·Ωª”⁄µ„A£®0 , 2£©£¨”Γª¥Œ∫Ø ˝y£Ωx©Å3µƒÕºœÛl
”Îy÷·Ωª”⁄µ„A£®0 , 2£©£¨”Γª¥Œ∫Ø ˝y£Ωx©Å3µƒÕºœÛl![]() Ωª”⁄µ„E£®m ,©Å5£©£Æ
Ωª”⁄µ„E£®m ,©Å5£©£Æ
£®1£©m=__________£ª
£®2£©÷±œþl![]() ”Îx÷·Ωª”⁄µ„B£¨÷±œþl
”Îx÷·Ωª”⁄µ„B£¨÷±œþl![]() ”Îy÷·Ωª”⁄µ„C£¨«ÛÀƒ±þ–ŒOBECµƒ√ʪ˝£ª
”Îy÷·Ωª”⁄µ„C£¨«ÛÀƒ±þ–ŒOBECµƒ√ʪ˝£ª
£®3£©»ÁÕº2£¨“—÷™æÿ–ŒMNPQ£¨PQ£Ω2£¨NP£Ω1£¨M£®a£¨1£©£¨æÿ–ŒMNPQµƒ±þPQ‘⁄x÷·…œ∆Ω“∆£¨»Ùæÿ–ŒMNPQ”Î÷±œþl![]() ªÚl
ªÚl![]() ”–Ωªµ„£¨÷±Ω”–¥≥ˆaµƒ»°÷µ∑∂Œß_____________________________
”–Ωªµ„£¨÷±Ω”–¥≥ˆaµƒ»°÷µ∑∂Œß_____________________________
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨‘⁄ABCD÷–£¨”√÷±≥þ∫Õ‘≤πÊ◊˜°œBADµƒ∆Ω∑÷œþAGΩªBC”⁄µ„E.»ÙBF£Ω12£¨AB£Ω10£¨‘ÚAEµƒ≥§Œ™(°°°°)

A. 16B. 15C. 14D. 13
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
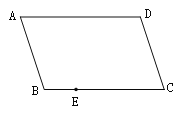
°æƒø°ø»ÁÕº£¨Àƒ±þ–ŒABCD «∆Ω––Àƒ±þ–Œ£¨E «BC±þ…œ“ªµ„£¨÷ª”√“ª∞—ŒÞøÃ∂»µƒ÷±≥þ‘⁄AD±þ…œ◊˜µ„F£¨ πµ√DF=BE.
£®1£©◊˜≥ˆ¬˙◊„“‚µƒµ„F£¨ºÚ“™Àµ√˜ƒ„µƒ◊˜Õºπ˝≥ãª
£®2£©“¿æðƒ„µƒ◊˜Õº£¨÷§√˜£∫DF=BE.
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øŒª”⁄ƒœ∞∂«¯ª∆ˈ€ÎµƒŒƒ∑ÂÀ˛£¨”–◊≈°∞∆Ω∞≤±¶À˛°±÷Æ≥∆£Æƒ≥–£ ˝—ß…ÁÕ≈∂‘∆‰∏þ∂» ABΩ¯––¡À≤‚¡ø£Æ»ÁÕº£¨À˚√«¥”À˛µ◊Aµƒµ„B≥ˆ∑¢£¨—ÿÀÆ∆Ω∑ΩœÚ––◊þ¡À13√◊£¨µΩ¥Ôµ„C£¨»ª∫Û—ÿ–±∆¬CDºÃ–¯«∞Ω¯µΩ¥Ôµ„D¥¶£¨“—÷™DC=BC£Æ‘⁄µ„D¥¶”√≤‚Ω«“«≤‚µ√À˛∂•Aµƒ—ˆΩ«Œ™42°„£®µ„A£¨B£¨C£¨D£¨E‘⁄Õ¨“ª∆Ω√ʃ⁄£©£Æ∆‰÷–≤‚Ω«“«º∞∆‰÷ߺÐDE∏þ∂»‘ºŒ™0.5√◊£¨–±∆¬CDµƒ∆¬∂»£®ªÚ∆¬±»£©i=1£∫2.4£¨ƒ«√¥Œƒ∑ÂÀ˛µƒ∏þ∂»AB‘ºŒ™£® £©£®sin42°„°÷0.67£¨cos42°„°÷0.74£¨tan42°„°÷0.90£©
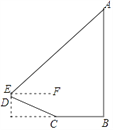
A. 22.5 √◊ B. 24.0 √◊ C. 28.0 √◊ D. 33.3 √◊
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø°æ‘ƒ∂¡¿ÌΩ‚°ø∂‘”⁄»Œ“‚’˝ µ ˝a°¢b£¨“ÚŒ™![]() °ð0£¨À˘“‘
°ð0£¨À˘“‘![]()
![]() °ð0£¨À˘“‘
°ð0£¨À˘“‘![]() °ð2
°ð2![]() £¨÷ª”–µ±
£¨÷ª”–µ±![]() ±£¨µ»∫≈≥…¡¢£Æ
±£¨µ»∫≈≥…¡¢£Æ
°æªÒµ√Ω·¬€°ø‘⁄![]() °ð2
°ð2![]() £®a°¢bæ˘Œ™’˝ µ ˝£©÷–£¨»Ù
£®a°¢bæ˘Œ™’˝ µ ˝£©÷–£¨»Ù![]() Œ™∂®÷µ
Œ™∂®÷µ![]() £¨‘Ú
£¨‘Ú![]() °ð2
°ð2![]() £¨÷ª”–µ±
£¨÷ª”–µ±![]() ±£¨
±£¨ ![]() ”–◊Ó–°÷µ2
”–◊Ó–°÷µ2![]() £Æ
£Æ
∏˘æð…œ ˆƒ⁄»ð£¨ªÿ¥œ¬¡–Œ £∫»Ù![]() >0£¨÷ª”–µ±
>0£¨÷ª”–µ±![]() = ±£¨
= ±£¨ ![]() ”–◊Ó–°÷µ £Æ
”–◊Ó–°÷µ £Æ
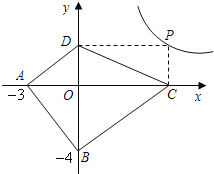
°æÃΩÀ˜”¶”√°ø»ÁÕº£¨“—÷™A£®£≠3£¨0£©£¨B£®0£¨£≠4£©£¨PŒ™À´«˙œþ![]() £®
£®![]() £æ0£©…œµƒ»Œ“‚“ªµ„£¨π˝µ„P◊˜PC°Õx÷·”⁄µ„C£¨PD°Õy÷·”⁄µ„D£Æ«ÛÀƒ±þ–ŒABCD√ʪ˝µƒ◊Ó–°÷µ£¨≤¢Àµ√˜¥À ±Àƒ±þ–ŒABCDµƒ–Œ◊¥£Æ
£æ0£©…œµƒ»Œ“‚“ªµ„£¨π˝µ„P◊˜PC°Õx÷·”⁄µ„C£¨PD°Õy÷·”⁄µ„D£Æ«ÛÀƒ±þ–ŒABCD√ʪ˝µƒ◊Ó–°÷µ£¨≤¢Àµ√˜¥À ±Àƒ±þ–ŒABCDµƒ–Œ◊¥£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™M£Ω£®a£´24£©x3©Å10x2£´10x£´5 «πÿ”⁄xµƒ∂˛¥Œ∂ýœÓ Ω£¨«“∂˛¥ŒœÓœµ ˝∫Õ“ª¥ŒœÓœµ ˝∑÷±Œ™b∫Õc£¨‘⁄ ˝÷·…œA°¢B°¢C»˝µ„À˘∂‘”¶µƒ ˝∑÷± «a°¢b°¢c£Æ
![]()
£®1£©‘Úa£Ω £¨b£Ω £¨c£Ω £Æ
£®2£©”–“ª∂ص„P¥”µ„A≥ˆ∑¢£¨“‘√ø√Î4∏ˆµ•ŒªµƒÀŸ∂»œÚ”“‘À∂Ø£¨∂ý…Ÿ√Î∫Û£¨PµΩA°¢B°¢Cµƒæý¿Î∫ÕŒ™40∏ˆµ•Œª£ø
£®3£©‘⁄£®2£©µƒÃıº˛œ¬£¨µ±µ„P“∆∂ØµΩµ„B ±¡¢º¥µÙÕ∑£¨ÀŸ∂»≤ª±‰£¨Õ¨ ±µ„T∫Õµ„Q∑÷±¥”µ„A∫Õµ„C≥ˆ∑¢£¨œÚ◊Û‘À∂Ø£¨µ„TµƒÀŸ∂»1∏ˆµ•Œª/√Σ¨µ„QµƒÀŸ∂»5∏ˆµ•Œª/√Σ¨…˵„P°¢Q°¢TÀ˘∂‘”¶µƒ ˝∑÷± «xP°¢xQ°¢xT£¨µ„Q≥ˆ∑¢µƒ ±º‰Œ™t£¨µ±![]() £ºt£º
£ºt£º![]() ±£¨«Û2|xP©ÅxT|£´|xT©ÅxQ|£´2|xQ©ÅxP|µƒ÷µ£Æ
±£¨«Û2|xP©ÅxT|£´|xT©ÅxQ|£´2|xQ©ÅxP|µƒ÷µ£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
π˙º —ß–£”≈—° - ¡∑œ∞≤·¡–±Ì - ‘¡–±Ì
∫˛±± °ª•¡™Õ¯Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®∆Ωî | Õ¯…œ”–∫¶–≈œ¢æŸ±®◊®«¯ | µÁ–≈’©∆≠柱®◊®«¯ | …Ê¿˙ ∑–ÈŒÞ÷˜“”–∫¶–≈œ¢æŸ±®◊®«¯ | …Ê∆Û«÷»®æŸ±®◊®«¯
Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®µÁª∞£∫027-86699610 柱®” œ‰£∫58377363@163.com