
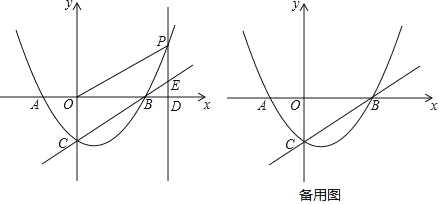
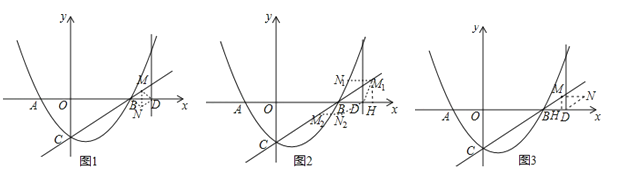
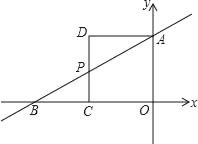
����Ŀ����ͼ��������y=ax2+bx��2�ĶԳ�����ֱ��x=1����x�ύ��A��B���㣬��y�ύ�ڵ�C����A������Ϊ����2��0������PΪ�������ϵ�һ�����㣬����P��PD��x���ڵ�D����ֱ��BC�ڵ�E��
��1���������߽���ʽ��
��2������P�ڵ�һ�����ڣ���OD=4PEʱ�����ı���POBE�������
��3���ڣ�2���������£�����MΪֱ��BC��һ�㣬��NΪƽ��ֱ������ϵ��һ�㣬�Ƿ���������ĵ�M�͵�N��ʹ���Ե�B��D��M��NΪ������ı��������Σ������ڣ�ֱ��д����N�����ꣻ�������ڣ���˵�����ɣ�
���𰸡�(1) �����߽���ʽΪy=![]() x2��
x2��![]() x��2��(2)
x��2��(2)![]() ;(3) ��N��
;(3) ��N��![]() ����
����![]() ����4.6��
����4.6��![]() ����5��
����5��![]() ����
����![]() ����5+
����5+![]() ��
��![]() �����Ե�B��D��M��NΪ������ı��������Σ�
�����Ե�B��D��M��NΪ������ı��������Σ�
�������������������1����������![]() �ĶԳ�����ֱ��x=1��A����2��0�����������ϣ������з��̼��ɵõ����ۣ�
�ĶԳ�����ֱ��x=1��A����2��0�����������ϣ������з��̼��ɵõ����ۣ�
��2�����ݺ�������ʽ�õ�B��4��0����C��0����2�������BC�Ľ���ʽ����D��m��0�����õ�E��m��![]() ����P��m��
����P��m��![]() ����������֪�����з��̵õ�m=5��m=0����ȥ�������D��P��E�����꣬���������ε������ʽ���ɵõ����ۣ�
����������֪�����з��̵õ�m=5��m=0����ȥ�������D��P��E�����꣬���������ε������ʽ���ɵõ����ۣ�
��3����M��n��![]() ��������BDΪ�Խ��ߣ��������ε����ʵõ�MN��ֱƽ��BD�����n��ֵ�����ǵõ�N������������BDΪ�ߣ��������ε����ʵõ�MN��BD��MN=BD=MD=1����M��MH��x����H�����ݹ��ɶ����з��̼��ɵõ����ۣ�
��������BDΪ�Խ��ߣ��������ε����ʵõ�MN��ֱƽ��BD�����n��ֵ�����ǵõ�N������������BDΪ�ߣ��������ε����ʵõ�MN��BD��MN=BD=MD=1����M��MH��x����H�����ݹ��ɶ����з��̼��ɵõ����ۣ�
�����������1����������![]() �ĶԳ�����ֱ��x=1��A����2��0�����������ϣ�
�ĶԳ�����ֱ��x=1��A����2��0�����������ϣ�
��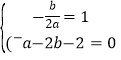 ����ã�
����ã�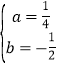 ��
��
�������߽���ʽΪ![]() ��
��
��2����![]() =0����ã�x1=��2��x2=4����x=0ʱ��y=��2��
=0����ã�x1=��2��x2=4����x=0ʱ��y=��2��
��B��4��0����C��0����2������BC�Ľ���ʽΪy=kx+b������![]() ����ã�
����ã�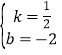 ��
��
��![]() ��
��
��D��m��0������DP��y�ᣬ
��E��m��![]() ����P��m��
����P��m��![]() ����
����
��OD=4PE��
��m=4��![]() ��
��![]() ��
��
��m=5��m=0����ȥ����
��D��5��0����P��5��![]() ����E��5��
����E��5��![]() ����
����
���ı���POBE�����=S��OPD��S��EBD=![]() ��5��
��5��![]() ��
��![]() ��1��
��1��![]() =
=![]() ��
��
��3�����ڣ���M��n��![]() ����
����
����BDΪ�Խ��ߣ���ͼ1��
���ı���BNDM�����Σ�
��MN��ֱƽ��BD��
��n=4+![]() =
=![]() ��
��
��M��![]() ��
��![]() ����
����
��M��N����x��Գƣ�
��N��![]() ����
����![]() ����
����
����BDΪ�ߣ���ͼ2��
���ı���BNDM�����Σ�
��MN��BD��MN=BD=MD=1��
��M��MH��x����H��
��MH2+DH2=DM2����![]() ��
��
��n1=4���������⣩��n2=5.6��
��N��4.6��![]() ����ͬ��
����ͬ��![]() ��
��
��n1=![]() ���������⣬��ȥ����n2=
���������⣬��ȥ����n2=![]() ��
��
��N��![]() ��
��![]() ����
����
����BDΪ�ߣ���ͼ3����M��MH��x����H��
��MH2+BH2=BM2����![]() ��
��
��n1=![]() ��n2=
��n2=![]() ���������⣬��ȥ����
���������⣬��ȥ����
��N��![]() ��
��![]() ����
����
������������N��![]() ����
����![]() ����4.6��
����4.6��![]() ����
����![]() ��
��![]() ����
����![]() ��
��![]() �����Ե�B��D��M��NΪ������ı��������Σ�
�����Ե�B��D��M��NΪ������ı��������Σ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�һ�κ���y=mx+n��m��0����ͼ���뷴��������y=![]() ��k��0����ͼ���ڵ�һ���������ڵ�A��B���㣬��y�ύ�ڵ�C������B��BM��x�ᣬ����ΪM��BM=OM��OB=2
��k��0����ͼ���ڵ�һ���������ڵ�A��B���㣬��y�ύ�ڵ�C������B��BM��x�ᣬ����ΪM��BM=OM��OB=2![]() ����A��������Ϊ4��
����A��������Ϊ4��
��1����÷�����������һ�κ����Ľ���ʽ��
��2������MC�����ı���MBOC�������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����6��С������ֽƬ����ͼ1��ʾ����ͼ2��ʾ�ķ�ʽ���ص��ķ��ڳ�����ABCD�ڣ�δ�����ǵIJ���ǡ�÷ָ�Ϊ���������Σ�����ֱ�ΪS1��S2����֪С������ֽƬ�ij�Ϊa����Ϊb����a>b����AB���Ȳ����BC�䳤ʱ����6��С������ֽƬ������ͬ���ķ�ʽ�����µij�����ABCD�ڣ�S1��S2�IJ��ܱ��ֲ��䣬��a��b����Ĺ�ϵ��

A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ij�µ�������Ȧ�������ڵ�������a��b��c������������ǵĺ�Ϊ39�����������������е��Ų��������ǣ�������
A. ![]() B.
B. 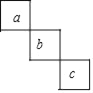 C.
C. 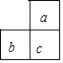 D.
D. 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��������A��B��C���㣬��A�͵�B���20����λ�����ҵ�A��B��ʾ����������Ϊ�෴����AC��36����������һ����P�ӵ�A��������ÿ��1����λ���ȵ��ٶ����������յ�C�ƶ������ƶ�ʱ��Ϊt�룮
![]()
��1����A��ʾ������������ ������B��ʾ������������ ������C��ʾ������������ ����
��2������P�˶�����Bʱ����Q�ӵ�O��������ÿ��6����λ���ȵ��ٶ��������ڵ�O�͵�C֮�������˶���
����tΪ��ֵʱ����Q��һ�����P�غϣ�
�ڵ���P�˶�����Cʱ����Q���˶�ֹͣ�����ʱ��Qһ���˶��˶��ٸ���λ���ȣ��������ʱ��Q������������ʾ����������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��OΪֱ��AB��һ�㣬��COE=90��,OFƽ�֡�AOE.
��1������COF=40�������BOE�Ķ���.
��2������COF=����0�㣼����90���������BOE=______���ú�����ʽ�ӱ�ʾ��.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
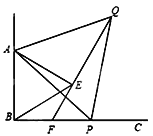
����Ŀ����ͼ�� ��֪��ABC��90�㣬��PΪ����BC������һ��(��P���B���غ�)���ֱ���AB��APΪ���ڡ�ABC���ڲ����ȱߡ�ABE�͡�APQ������QE���ӳ���BP�ڵ�F. ��˵������1����ABP�ա�AEQ����2��EF��BF
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����x��һԪ���η���x2��x+a��1=0��
��1����a=��11ʱ����������̣�
��2�����������������ʵ����x1��x2����a��ȡֵ��Χ��
��3������������ʵ����x1��x2����[2+x1��1��x1��][2+x2��1��x2��]=9����a��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ֱ������ϵ�У�ֱ��AB�ֱ���x�ᡢy�ύ��B��A���㣬OA��OB�ij��ǹ���x��һԪ���η���x2��12x+32=0������ʵ��������OB��OA����OAΪһ������ͼ��ʾ��������AOCD��CD��AB�ڵ�P��
��1����ֱ��AB�Ľ���ʽ��
��2����x�����Ƿ����һ��Q��ʹ��P��C��QΪ���������������ADP���ƣ������ڣ����Q���ꣻ����˵�����ɣ�
��3����N��ƽ����һ���㣬��y�����Ƿ���ڵ�M��ʹ����A��C��M��NΪ������ı��������Σ������ڣ���ֱ��д����M�����ꣻ������˵�����ɣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com