【题目】我市某储运部紧急调拨一批物资，调进物资共用4小时，调进物资2小时后开始调出物资（调进物资与调出物资的速度均保持不变）．储运部库存物资S（吨）与时间t（小时）之间的函数关系如图所示，这批物资从开始调进到全部调出需要的时间是_________小时.
科目：初中数学 来源： 题型：
【题目】将6张小长方形纸片（如图1所示）按图2所示的方式不重叠的放在长方形ABCD内，未被覆盖的部分恰好分割为两个长方形，面积分别为S1和S2．已知小长方形纸片的长为a，宽为b，且a>b．当AB长度不变而BC变长时，将6张小长方形纸片还按照同样的方式放在新的长方形ABCD内，S1与S2的差总保持不变，则a，b满足的关系是
A. 
B. 
C. 
D. 
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图， 已知∠ABC＝90°，点P为射线BC上任意一点(点P与点B不重合)，分别以AB、AP为边在∠ABC的内部作等边△ABE和△APQ，连接QE并延长交BP于点F. 试说明：（1）△ABP≌△AEQ；（2）EF＝BF
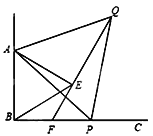
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知关于x的一元二次方程x2﹣x+a﹣1=0．
（1）当a=﹣11时，解这个方程；
（2）若这个方程有两个实数根x1，x2，求a的取值范围；
（3）若方程两个实数根x1，x2满足[2+x1（1﹣x1）][2+x2（1﹣x2）]=9，求a的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知AB=AC，DE垂直平分AB交AC、AB于E、D两点，若AB=12cm，BC=10cm，∠A=50°，求△BCE的周长和∠EBC的度数.
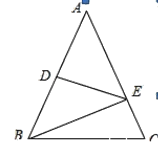
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】我市举行“第十七届中小学生书法大赛”作品比赛，已知每幅参赛作品成绩记为
，组委会从1000幅书法作品中随机抽取了部分参赛作品，统计了它们的成绩，并绘制成如下统计图表.
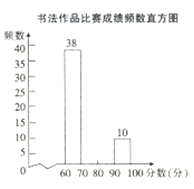
分数段 | 频数 | 百分比 |
| 38 | 0.38 |
| ______ | 0.32 |
| ______ | ______ |
| 10 | 0.1 |
合计 | ______ | 1 |
根据上述信息，解答下列问题：
(1)请你把表中的数据填写完整.
(2)补全书法作品比赛成绩频数直方图.
(3)若80分(含80分)以上的书法作品将被评为等级奖，试估计全市获得等级奖的幅数.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在△ABC中，AB=AC=10cm，BC=16cm，现点P从点B出发，沿BC向C点运动，运动速度为
m/s，若点P的运动时间为t秒，则当△ABP是直角三角形时，时间t的值可能是_____．
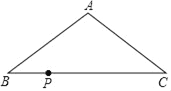
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在直角坐标系中，直线AB分别与x轴、y轴交于B、A两点，OA、OB的长是关于x的一元二次方程x2﹣12x+32=0的两个实数根，且OB＞OA，以OA为一边作如图所示的正方形AOCD，CD交AB于点P．
（1）求直线AB的解析式；
（2）在x轴上是否存在一点Q，使以P、C、Q为顶点的三角形与△ADP相似？若存在，求点Q坐标；否则，说明理由；
（3）设N是平面内一动点，在y轴上是否存在点M，使得以A、C、M、N为顶点的四边形是菱形？若存在，请直接写出点M的坐标；否则，请说明理由．
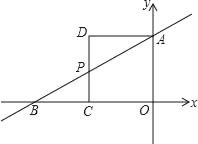
查看答案和解析>>
科目：初中数学 来源： 题型：
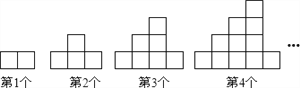
【题目】如图，下列图案均是由长度相同的火柴按一定的规律拼搭而成，围成的每个小正方形面积为1
.第一个图案面积为2，第二个图案面积为4，第三个图案面积为7，…依此规律，第8个图案面积为（ ）
A. 34 B. 35 C. 36 D. 37
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
