
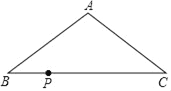
【题目】如图,在△ABC中,AB=AC=10cm,BC=16cm,现点P从点B出发,沿BC向C点运动,运动速度为![]() m/s,若点P的运动时间为t秒,则当△ABP是直角三角形时,时间t的值可能是_____.
m/s,若点P的运动时间为t秒,则当△ABP是直角三角形时,时间t的值可能是_____.
【答案】32s或50s
【解析】分析:分∠APB与∠PAB两种情况进行分类讨论,当∠APB=90°时,AP⊥BC,根据等腰三角形的性质可得出BP=CP,故可得出t的值;当∠PAB=90°时,过点A作AE⊥BC交BC于点E,由等腰三角形的性质得出BE=CE,用t表示出PE的长,再由勾股定理即可得出结论.
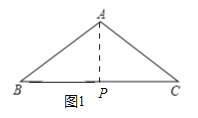
详解:如图1中,当∠APB=90°时,AP⊥BC.
∵AB=AC,AP⊥BC,∴BP=CP=![]() BC=8cm,∴
BC=8cm,∴![]() t=8,解得:t=32秒;
t=8,解得:t=32秒;
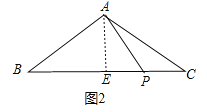
如图2中,当∠PAB=90°时,过点A作AE⊥BC交BC于点E.
∵AB=AC,AE⊥BC=8,
∴BE=CE=![]() BC=8,∴PE=BP﹣BE=
BC=8,∴PE=BP﹣BE=![]() t﹣8.
t﹣8.
在Rt△AEC中,AE2=AC2﹣CE2,即AE2=102﹣82,解得:AE=6cm.
在Rt△PAB中,AP2=BP2﹣AB2.在Rt△AEP中,AE2=PE2+AE2,∴(![]() t)2﹣100=(
t)2﹣100=(![]() t﹣8)2+36,解得:t=50(秒).
t﹣8)2+36,解得:t=50(秒).
综上所述:t的值为32秒或50秒.
故答案为:32s或50s.


科目:初中数学 来源: 题型:
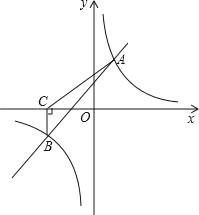
【题目】如图,一次函数y=kx+b与反比例函数y=![]() 的图象交于A(2,3),B(﹣3,n)两点.
的图象交于A(2,3),B(﹣3,n)两点.
(1)求一次函数与反比例函数的表达式;
(2)根据所给条件,请直接写出不等式kx+b>![]() 的解集;
的解集;
(3)过点B作BC⊥x轴,垂足为C,求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为3 cm,P、Q分别从B、A出发沿BC,AD方向运动,P点的运动速度是1 cm/秒,Q点的运动速度是2 cm/秒。连接AP并过Q作QE⊥AP垂足为E。
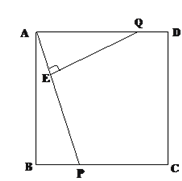
(1)求证:△ABP∽△QEA ;
(2)当运动时间t为何值时,△ABP≌△QEA;
(3)设△QEA的面积为y,用运动时间t表示△QEA的面积y。(不要求考虑t的取值范围)
(提示:解答(2)(3)时可不分先后)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某储运部紧急调拨一批物资,调进物资共用4小时,调进物资2小时后开始调出物资(调进物资与调出物资的速度均保持不变).储运部库存物资S(吨)与时间t(小时)之间的函数关系如图所示,这批物资从开始调进到全部调出需要的时间是_________小时.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法错误的有( )
①有理数包括正有理数和负有理数; ②绝对值等于它本身的数是非负数;③若|b|=|﹣5|,则b=-5 ; ④当b=2时,5﹣|2b﹣4|有最小值是5;⑤若![]() 、
、![]() 互为相反数,则
互为相反数,则![]() ;⑥
;⑥![]() 是关于
是关于![]() 、
、![]() 的六次三项式.
的六次三项式.
A.2个B.3个C.4个D.5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在直角坐标系中,一次函数的图象l![]() 与y轴交于点A(0 , 2),与一次函数y=x﹣3的图象l
与y轴交于点A(0 , 2),与一次函数y=x﹣3的图象l![]() 交于点E(m ,﹣5).
交于点E(m ,﹣5).
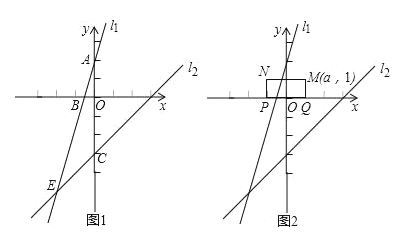
(1)m=__________;
(2)直线l![]() 与x轴交于点B,直线l
与x轴交于点B,直线l![]() 与y轴交于点C,求四边形OBEC的面积;
与y轴交于点C,求四边形OBEC的面积;
(3)如图2,已知矩形MNPQ,PQ=2,NP=1,M(a,1),矩形MNPQ的边PQ在x轴上平移,若矩形MNPQ与直线l![]() 或l
或l![]() 有交点,直接写出a的取值范围_____________________________
有交点,直接写出a的取值范围_____________________________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,用直尺和圆规作∠BAD的平分线AG交BC于点E.若BF=12,AB=10,则AE的长为( )

A. 16B. 15C. 14D. 13
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】位于南岸区黄桷垭的文峰塔,有着“平安宝塔”之称.某校数学社团对其高度 AB进行了测量.如图,他们从塔底A的点B出发,沿水平方向行走了13米,到达点C,然后沿斜坡CD继续前进到达点D处,已知DC=BC.在点D处用测角仪测得塔顶A的仰角为42°(点A,B,C,D,E在同一平面内).其中测角仪及其支架DE高度约为0.5米,斜坡CD的坡度(或坡比)i=1:2.4,那么文峰塔的高度AB约为( )(sin42°≈0.67,cos42°≈0.74,tan42°≈0.90)
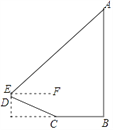
A. 22.5 米 B. 24.0 米 C. 28.0 米 D. 33.3 米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用配方法解下列方程时,配方错误的是( )
A. x2+2x﹣99=0化为(x+1)2=100
B. 2x2﹣7x﹣4=0化为![]()
C. x2+8x+9=0化为(x+4)2=25
D. 3x2﹣4x﹣2=0化为(x-![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com